引言
紧固件是用于把两个或两个以上的零件(构件)连接成一个整体的机械零件,发展到今天紧固件已形成包括螺栓、螺柱(桩)、螺钉、螺母、垫圈、铆钉、销、挡圈和嵌入件等在内的一系列产品。其中,螺纹连接构造简单、成本较低、安装方便,使用不受被连接材料限制,因而应用广泛。
螺栓、螺母或内外螺纹构件,其连接设计要求(目标)主要根据被连接件的具体要求而定。选择螺栓(外螺纹)、螺母(内螺纹)类型和结构时,要保证足够的承载能力,要满足装拆的方便性或不拆卸的要求,以确保质量检验的便利性[1]。应按有关设计手册计算,以保证足够的承载能力,一旦选择了螺栓(外螺纹)、螺母(内螺纹)和螺纹连接副,其各自的性能强度应符合GB/T 3098.1—2010《紧固件机械性能螺栓、螺钉和螺柱》、GB/T 3098.2—2015《紧固件机械性能螺母》规定的性能等级。螺栓(外螺纹)、螺母(内螺纹)连接副的性能等级搭配设计应符合GB/T 3098.2—2015“螺母性能等级与搭配使用的螺栓、螺钉或螺柱的最高性能等级”或HB 6443—2008《螺母通用规范》“螺母的强度等级等于与该螺母相配的最高性能等级的螺栓的抗拉强度”附录A“螺母强度等级”规定,上述两个螺母标准共同点是连接件搭配螺母的性能等级等于与螺母相配的最高性能等级的螺栓(外螺纹)件性能等级,这样可以充分发挥螺栓的强度性能,并可提供一个最大的预紧力。对螺纹按标准选取,不用校对螺纹强度;若不按标准选取,需要校对螺纹强度。对螺纹连接的设计,通常希望在超拧的情况下,螺栓、螺母连接副中,螺杆断裂是预期的失效形式(GB/T 3098.2—2015附录A)。
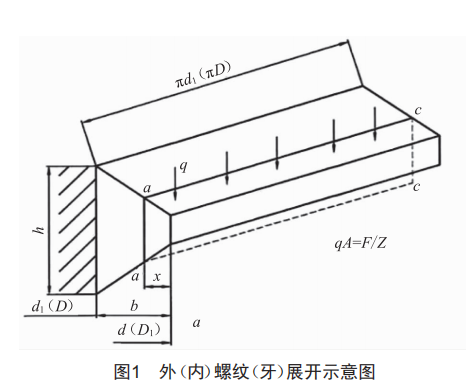
由于对精确度了解不够,目前为保证零件连接可靠性,在设计时只得用降低许用应力或设定一个系数的方法来校核。而螺纹(牙)校核主要是采用sopwith和yamatoto提出的将螺纹展开看成悬臂梁(图1)的理论[2—5],按悬臂梁结构假设进行弯曲、剪切、挤压,应力分别按材料力学解析法进行校核,不超过各自许用应力,即螺纹(牙)满足安全强度条件。那么这种校核符合实际吗?能发挥材料的潜力吗?螺纹展开类似悬臂梁吗?
本文以材料力学、弹性力学理论为依据,以试验结果为分析基础,根据GB/T 3098.2—2015标准规定内螺纹高度(螺母厚度)H≥0.8D、螺纹有效长度≥0.6D(D为内螺纹基本大径)以及螺纹断裂形貌特征,对螺纹悬臂梁假设进行探讨,提出螺纹悬臂梁假设不符合材料力学、弹性力学定义悬臂梁的要素,采用材料力学的悬臂梁弯曲应力、剪切应力公式,不符合试验结果。在此基础上,笔者提出了螺纹环形受剪力学模型,认为螺纹(牙)主要受剪力,只校核切应力T≤[T]([T]为许用剪切应力)即可满足螺纹设计要求。同时采用科学类比方法,发现内外螺纹受力等效于垫圈冲孔力学应力状态,所以可以借用垫圈冲孔应力状态来进行对比分析。
1材料力学定义悬臂梁结构要素
外螺纹、内螺纹强度校核都是延用sopwith将螺纹展开看作悬臂梁结构进行的,即对弯曲正应力σW、剪应力T、挤压应力σP和修正系数k分别进行校核[1]:
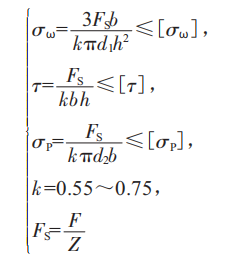
按材料力学[6]弯曲理论解析法得出,存在剪应力下的弯曲为横力弯曲,横力弯曲的剪应力为纯剪应力的1.5倍,即:
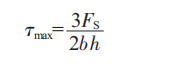
横力弯曲是在纯弯曲正应力计算的基础上引入了两个假设,一个是平面设计,另一个是认为纵向纤维面无应力。公式(1)(2)是针对梁截面高度(牙厚)远小于跨度(牙高)的实际梁,这种梁才有可能满足平面假设,才会与实际偏差非常小[7]。第二假设也是只有高度/跨度(牙厚/牙高)比值远小于1,纵向正应力与弯曲正应力比值才非常小,才可以忽略不计纵向正应力[7]。
而螺纹(牙)恰恰相反,牙厚大于牙高,第二点假设悬臂梁是一端开口,一端固定,而真实的螺纹(牙)是环形闭合的,故公式(1)(2)与实际有出入。
用悬臂梁结构弯曲正应力和切应力假设计算得到的公式(1)(2)与实际有出入,所以用悬臂梁做假设校核强度是不精确的。为了满足校核的要求,只有过大提高安全系数K来保证螺纹连接强度的安全性,这不利于挖掘螺纹工件材料、性能等潜能,也不能为螺纹失效分析提供可靠的理论依据。
2建立螺纹环形剪切力学模型
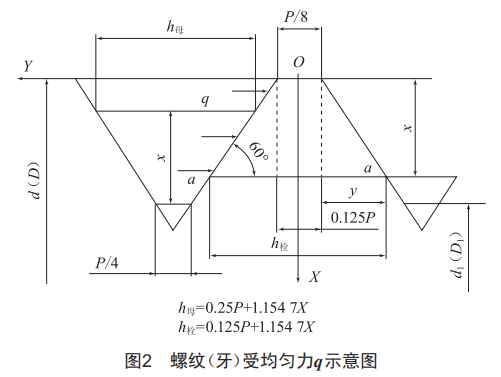
螺纹连接时外螺纹(牙)受到内螺纹(牙)压力,可以假设压力均匀分布在牙侧面,均匀分布力为q,如图2所示。Fs(=qA)对外螺纹牙底圆周处会产生剪力和弯曲,剪力会引起切应力、弯曲会引起弯曲正应力,那螺纹断裂是弯曲正应力σmax≥σb,还是Tmax≥Tb时引起的(σb为材料抗拉强度、Tb为材料剪切强度)?下面来进行分析。
2.1螺纹断口宏观分析
试验设计:螺栓在受拉力时,螺纹杆部受正应力,螺纹受弯曲正应力、切应力、挤压应力。挤压应力较小,一般不计[7]。
采用M6×20GB/T5783,HRC31~32,σb=1070Mpa,性能满足GB/T 3098.1—2010要求的螺栓来进行试验。
为了让螺栓杆部不断裂,螺栓螺纹脱扣,螺母厚度设计小于0.6D,本次厚度H分别为1.5、2.0、2.5、3.0、3.5 mm,其余尺寸符合GB/T 6170—2015《1型六角螺母》标准要求,硬度为HRC23~26,机械性能满足标准GB/T 3098.2__2015要求。
试验方法:螺栓、螺母连接组合,模拟实际装配受力方式,用扭矩安装,如图3所示。
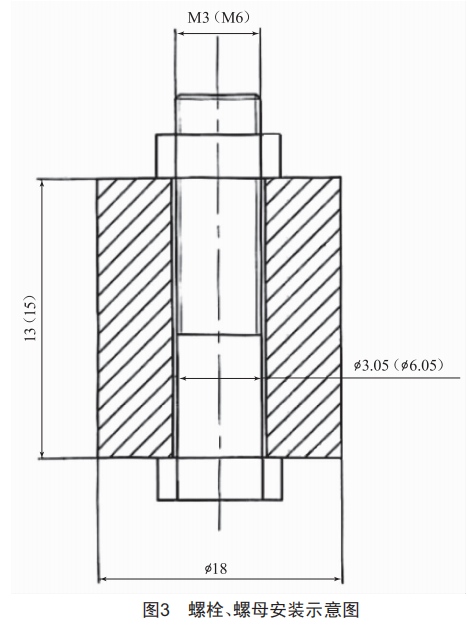
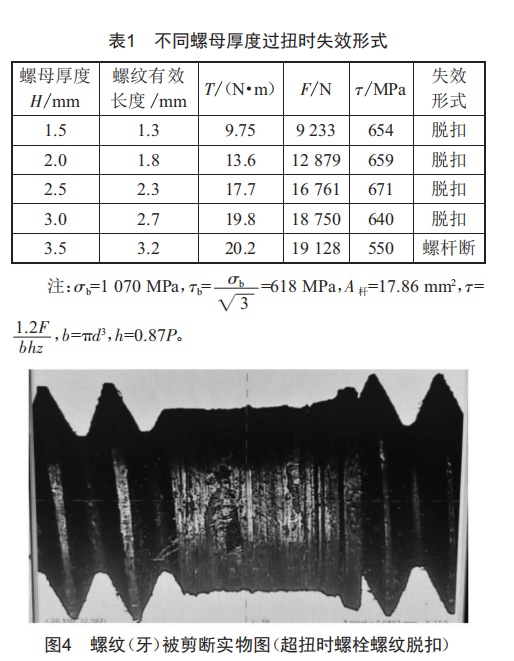
试验结果如表1所示。
在40倍投影仪上对断裂件进行宏观观测,如图4所示(螺母厚度H=3 mm),从断口来看是剪断的,若是弯曲过截断裂的断口,总体上来说特征与拉伸断裂断口相似,在弯曲断口上可以观察到明显的放射线或人字花样[8]。
当试样受弯曲载荷作用时,凸面受拉应力分布与拉伸相似,断裂部位存在塑性变形。断口上一般可以看到三个特征区域:纤维区、放射区和剪唇。凹面受压应力分布与单向压缩近似,有中间腰鼓型,试样中心应力为零。而实际螺纹(牙)断口不是弯曲正应力造成的形貌,图4未见放射线或人字花样及三个特征区域,断裂明显是由切应力引起,断面相对较为平滑,颜色较暗。
2.2剪切定义要素
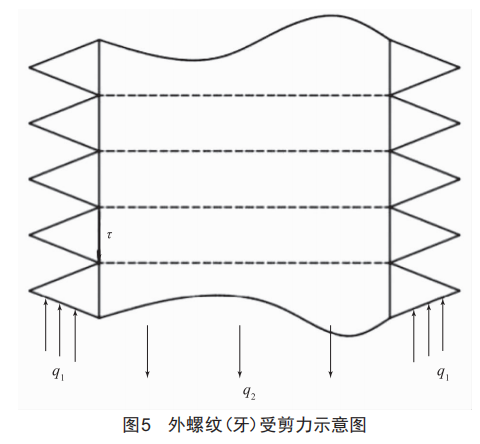
由试验中断口分析得知,断裂主要是剪断的,剪切的特点如下:作用于构件某一截面两侧的力,大小相等,方向相反,且相互平行,使构件这一截面(剪切面)的两部分发生相对错动的变形。而连接件外螺纹小径d1与内螺纹小径D1理论值一样,实际公差非常小,可以理解d1圆周处受大小相等、方向相反且相互平行的两个力,如图5所示,所以符合剪切定义要素。
3螺纹(牙)环形受剪力学模型切应力公式
3.1外螺纹受力形式类似于垫圈冲孔应力状态
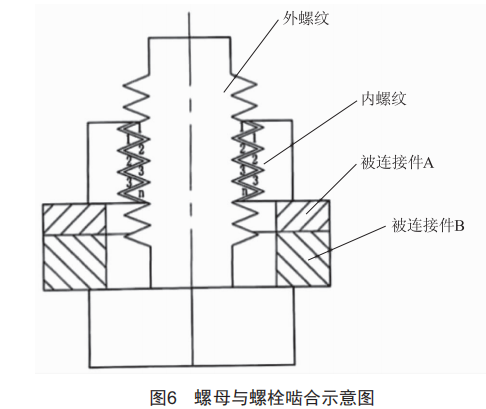
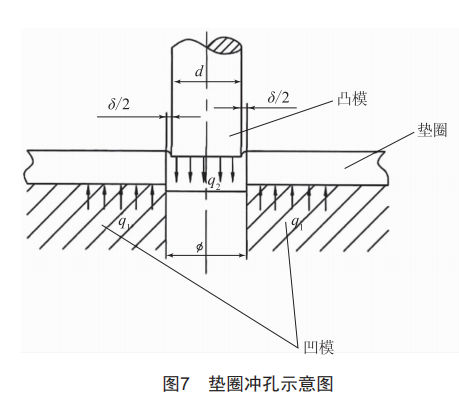
根据上面螺纹(牙)断裂形态得出结论:螺纹(牙)是被剪断的。根据试验结果提出螺纹(牙)环形剪切力学模型假设。如图5、图6所示,螺母拧紧时,螺栓杆部受到均匀载荷q2,外螺纹受到均匀载荷q1,q1与q2方向相反。外螺纹与螺母内螺纹牙个数基本一一对应,每个螺栓螺纹(牙)都是环形结构,类似多个重叠圆形薄板,受力形式等效于垫圈冲孔力学状态,如图7所示。可用科学研究的类比法来分析:内螺纹(牙)类似多个凹模,螺栓杆部在螺母(或螺栓)旋拧时受拉,类似多个凸模,每个外螺纹杆部的类似凸模连续对应每个内螺纹凹模。由于内螺纹小径D1与外螺纹小径d1配合公差非常小,和冲孔原理一样,都是圆周πd1处受弯受剪但主要受剪,最终是切应力T造成金属断裂分离。
3.2螺纹小径d1、D1与冲孔凹凸模单边间隙比较将外螺纹小径d1与内螺纹小径D1之间差值与垫圈冲孔凹凸模单边间隙进行比较,内螺纹小径D1按GB/T 197—2018《普通螺纹公差》规定:当0.2 mm≤P≤0.8 mm时,TD1(6)=433P—190P1.22;当P≥1 mm时,TD1(6)=230P0.7。其中,(6)为6级精度,TD1的单位为微米,具体数据如表2所示。
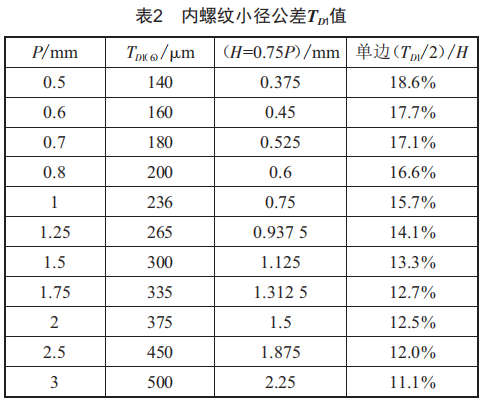
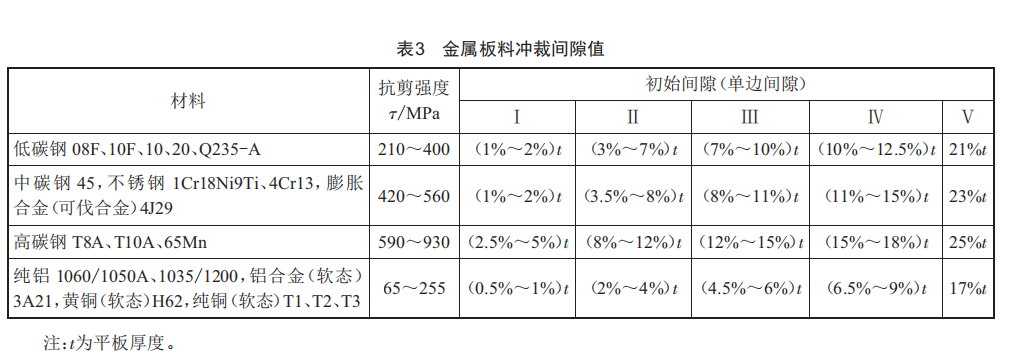
螺栓与螺母性能等级按GB/T 3098.2—2015搭配,螺母的性能级别与螺栓性能级别一样,如8级螺母配8.8级螺栓,螺纹公差一般按GB197 6H/6h配合[9]。6H/6h公差间隙与根部厚度0.75P比值(表2)与GB/T 16743—2010《冲裁间隙》标准中金属板料冲裁单边间隙值(表3、图7)进行比较,取垫圈T在590~930 Mpa这挡。
由表3可知,金属板料冲裁单边间隙值Ⅲ类(12%~15%)t、IV类(15%~18%)t。当P≤0.8 mm时内螺纹小径D1与外螺纹小径d1公差间隙处在Ⅳ类,当P≥1 mm处在Ⅲ类,都小于螺纹断裂部位厚度h。外螺纹底部d1牙厚0.87P,即t=0.87P,完全与冲孔垫圈凹凸模单边间隙一致。若板料要产生弯曲,凹凸模间隙必须满足1.05t~1.15t[10],而螺纹配合公差要求不满足1.05T~1.15T条件,所以不可能弯曲断裂。因此,科学类比法说明,配合安装后螺栓与螺母受力状态完全等效于冲孔垫圈受力状态,可以借鉴冲孔垫圈受力状态进行分析。
螺纹变形过程与冲孔垫圈受力过程一样,由以下几个过程组成:
1)弹性变形阶段:变形区产生弹性压缩、拉伸、弯曲等变形。
2)塑性变形阶段:旋拧螺栓或螺母,螺栓杆部继续受拉,螺纹(牙)切应力达到屈服极限,外螺纹在内螺纹作用下产生塑性剪切变形。
3)断裂阶段:螺栓杆部继续受拉,外螺纹(牙)应力达到了剪切强度极限Tb,在外螺纹根部d1圆周处产生微小裂纹。
结论
1)把螺纹(牙)展开视为悬臂梁,按悬臂梁进行强度校核,缺乏严密的理论依据和试验结果支撑。
2)以试验结果为依据,同时采用科学类比法,以内螺纹小径D1与外螺纹小径d1之间的公差间隙,对比冲裁平垫圈凹凸模单边间隙,由数据得出内螺纹与外螺纹配合连接受剪力状态等效垫圈冲孔受剪状态,即当A纹