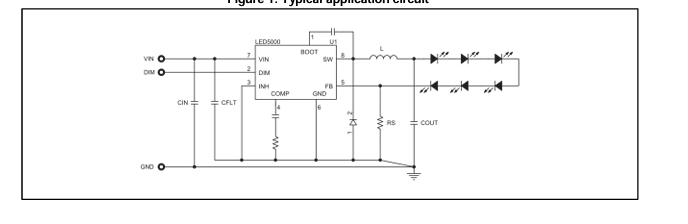
在数字信号处理领域,滤波器作为一种重要的工具,用于对信号进行筛选、增强或抑制特定频率成分。FIR(有限脉冲响应)滤波器和
IIR(无限脉冲响应)滤波器是其中最为常用的两种类型,它们在结构、性能、设计方法以及应用场景等方面存在诸多显著区别。深入了解这些区别,对于工程师在实际项目中选择合适的滤波器类型至关重要。
一、结构差异
FIR 滤波器的结构相对简单直观。它是一种非递归滤波器,其输出仅取决于当前和过去的输入信号,而与过去的输出信号无关。从数学表达式来看,FIR
滤波器的输出 y (n) 可以表示为输入信号 x (n) 的加权和,即:
y(n)=k=0∑N−1h(k)x(n−k)
其中,h (k) 是滤波器的单位脉冲响应系数,N 是滤波器的阶数。在硬件实现上,FIR 滤波器通常由延迟单元、乘法器和加法器组成。例如,一个简单的 3
阶 FIR 滤波器,需要 3 个延迟单元来存储过去的输入信号,3
个乘法器分别将当前和过去的输入信号与对应的系数相乘,最后通过加法器将乘积结果相加得到输出信号。这种结构使得 FIR
滤波器在稳定性方面具有天然优势,因为不存在反馈回路,不会因反馈信号的累积而导致系统不稳定。
相比之下,IIR 滤波器采用递归结构。其输出不仅依赖于当前和过去的输入信号,还与过去的输出信号有关。IIR
滤波器的数学表达式较为复杂,一般可以表示为:
y(n)=k=0∑Mb(k)x(n−k)−k=1∑Na(k)y(n−k)
其中,a (k) 和 b (k) 分别是与过去输出和输入信号相关的系数,M 和 N 分别是输入和输出部分的阶数。在硬件实现上,IIR
滤波器除了包含延迟单元、乘法器和加法器外,还存在反馈回路,将过去的输出信号反馈到输入端参与运算。这种递归结构使得 IIR
滤波器能够用较低的阶数实现较为复杂的滤波特性,但也带来了稳定性问题,若系数设置不当,反馈信号可能会不断累积,导致系统发散。
二、性能特点
FIR
滤波器在性能上具有线性相位特性,这是其显著优势之一。线性相位意味着信号通过滤波器后,不同频率成分的相位延迟与频率成正比,信号的波形不会发生失真。在对信号波形要求较高的应用中,如语音处理、图像传输等领域,FIR
滤波器的线性相位特性尤为重要。例如,在语音通信中,若使用非线性相位的滤波器,可能会导致语音信号的相位失真,使接收端听到的声音变得模糊、不自然。而 FIR
滤波器能够保证语音信号的相位一致性,还原出清晰、自然的语音。
IIR 滤波器在幅度特性方面表现出色,能够以较低的阶数实现陡峭的幅频响应,即在通带内保持信号幅度不变,在阻带内迅速衰减信号。这使得 IIR
滤波器在对信号频率选择性要求较高的场景中应用广泛,如在音频均衡器中,需要对不同频率的音频信号进行不同程度的增益或衰减,IIR
滤波器可以通过精心设计的系数,实现精确的频率响应,有效提升音频的音质。然而,IIR
滤波器的相位特性通常是非线性的,会导致信号在通过滤波器时产生相位失真,这在一些对相位敏感的应用中是一个明显的劣势。
三、设计方法
FIR
滤波器的设计方法丰富多样。常见的有窗函数法、频率采样法和等波纹最佳逼近法等。窗函数法是一种较为简单直观的设计方法,通过选择合适的窗函数(如矩形窗、汉宁窗、海明窗等)对理想低通滤波器的脉冲响应进行截断,从而得到
FIR
滤波器的系数。这种方法设计过程相对简单,易于理解和实现,但滤波器的性能(如阻带衰减、过渡带宽度等)受到窗函数类型和长度的限制。频率采样法是根据给定的频率响应采样值,通过内插公式来确定滤波器的系数,该方法适用于对滤波器频率响应有明确要求的设计场景。等波纹最佳逼近法则是基于切比雪夫逼近理论,在通带和阻带内使误差均匀分布,以获得最佳的逼近效果,这种方法能够设计出性能优良的
FIR 滤波器,但计算过程较为复杂,通常需要借助计算机软件实现。
IIR
滤波器的设计通常基于模拟滤波器的设计方法,如巴特沃斯滤波器、切比雪夫滤波器和椭圆滤波器等。首先设计出满足性能要求的模拟滤波器,然后通过双线性变换法或脉冲响应不变法等将其转换为数字
IIR 滤波器。巴特沃斯滤波器具有平坦的通带和单调下降的阻带特性,设计相对简单。切比雪夫滤波器分为 I 型和 II 型,I
型在通带内具有等波纹特性,阻带单调下降;II
型在阻带内具有等波纹特性,通带平坦。椭圆滤波器则在通带和阻带内都具有等波纹特性,能够以最小的阶数实现给定的性能指标。在将模拟滤波器转换为数字滤波器时,双线性变换法能够避免频率混叠问题,但会产生频率畸变;脉冲响应不变法能较好地保持模拟滤波器的频率响应形状,但可能会出现频率混叠现象,在设计时需要根据具体需求选择合适的转换方法。
四、应用场景
由于 FIR
滤波器具有线性相位和稳定的特性,在对信号相位要求严格的应用中得到广泛应用。在通信系统中,用于调制解调、信道均衡等环节,确保信号在传输过程中不失真。在图像信号处理中,对图像进行滤波去噪时,FIR
滤波器能够在去除噪声的同时,最大程度保持图像的边缘和细节信息,避免因相位失真导致图像模糊。
IIR
滤波器因其良好的频率选择性和较低的阶数要求,在音频处理、电力系统谐波分析等领域发挥着重要作用。在音频系统中,用于构建各种音频滤波器,如低通、高通、带通滤波器等,实现音频信号的分频、均衡等功能,提升音频质量。在电力系统中,用于检测和抑制谐波,通过设计合适的
IIR 滤波器,能够有效滤除电力信号中的谐波成分,保障电力系统的稳定运行。
FIR 滤波器和 IIR
滤波器各有优劣,在实际应用中,工程师需要根据具体的需求,综合考虑滤波器的结构、性能、设计方法等因素,选择最适合的滤波器类型,以实现最佳的信号处理效果。