全球半导体行业景气周期下行 预计2019H2回暖
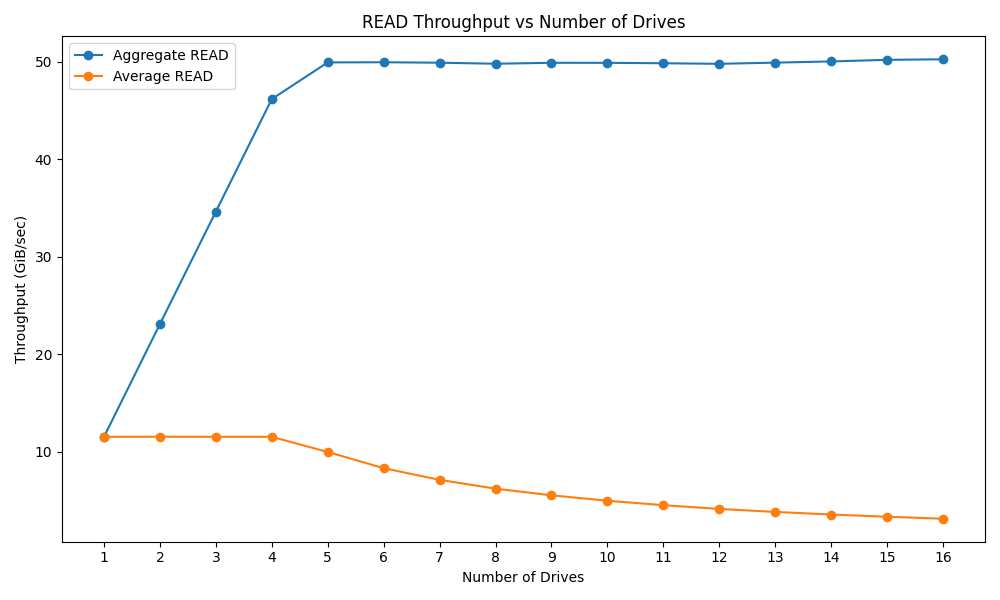
半导体指数走弱
费城半导体指数(SOX)是全球半导体业景气主要指标,2018年累计下跌7.81%。中国台湾半导体指数2018年累计下跌6.82%。申万半导体指数2018年累计下跌40.60%。
全球半导体销售额增速放缓,终端市场需求疲软
根据IC Insights 2018年11月数据,2018年上半年,IC市场的季度同比增长强劲,但从第三季度开始,IC市场同比增长率降至14%。随着内存市场的疲软,IC Insights预计第四季度IC市场同比增长率仅为6%。WSTS 2018年11月预估,2018与2019年全球半导体销售额分别年增15.9%与2.6%,达4779.36亿与4901.42亿美元。全球半导体销售额增速放缓主要是由于下游智能手机、数据中心、汽车等需求疲软。
库存周期处于历史高位
全球半导体行业前20公司2018Q3库存周转天数达到97天,超过历史高位。全球模拟半导体行业2018Q3库存周转天数达到106天。
中国大陆、韩国资本支出减少,念喊郑预计设备销售额2020年再创新高
SEMI 2018年11月将2018/2019年晶圆厂投资增长从8月份的预测的14%/7%下调至10%/-7%。SEMI对中国大陆地区和韩国2019年支出预测均下调至120亿美元(8月预测均为170亿美元)。SEMI 2018年12月预测2018年新的半导体制造设备的全球销售额预计将增加9.7%达到621亿美元(8月预测为627亿美元),预计2019年设备市场仔颂将收缩4.0%至596亿美元(8月预测为676亿美元),但2020年将增长20.7%,达到719亿美元,创历史新高。
预计2019H2开始回暖,重点关注设备与设计
从需求角度看,结合5G 2019/2020年商用的建设进展以及2019H2汽车行业有望进入补库存阶段,我们预计2019H2半导体行业下游需求有望回暖。从库存角度看,结合历史去库存时间2-3个季度,我们预计2019H2半导体行业库存将回落到正常水平。从资本支出看,考虑到未来5G、AI、IOT等需求确定性高,资本支出只是延迟,但并没有消失。根据SEMI预计,2018H2总体支出下降13%,2019H1下降16%,2019H2晶圆厂设备支出将大幅增加。综合需求、库存、资本支出等方面的考虑,我们认为全球半导体行业有望于2019年H2开始回暖,建议关注半导体细分领域龙头标的,设备:北方华创、长川科技;设计:圣邦股份、韦尔股份、兆易创新;功率IDM:扬杰科技,捷捷微电,闻泰科技。
风险分析:
5G建设进展不及预期,去库存不及预期,渗铅资本支出不及预期,半导体行业景气度复苏不及预期。
(文章来源:光大证券)
matlab实现欧拉法和RK-4方法的数值计算
程序已经写了,不过步长你得自己调,当步长较小时,计算时间会很长
另外,tend是时间的终值,你可以设小一些。因为解析解为10*cos(x),我设成pi,就是计算半个周期。
x''(t)=-x(t)
引入y1=x,y2=x',则
y1'=y2
y2'=-x=-y1
初始条件为:
y1(0)=10;
y2(0)=0;
将下面两行百分号之间的内容,保存成DiffEulerRk4.m
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function MaxDiffX=DiffEulerRk4(dt,PlotFlag)
%dt是步长
%PlotFlag是否作图
if nargin<1
dt=0.01;
end
if nargin<2
PlotFlag=0;
end
f=inline('[y(2);-y(1)]','t','y'); %微分方程的右边项
t0=0; %初始时刻
tend=pi; %计算的点数
tt=t0:dt:tend; %一系列离散的点
N=length(tt); %点数
y0=[10;0];
%%(1)欧拉法
EulerY=y0;
for i=2:N
EulerY(:,i)=EulerY(:,i-1)+dt*f(tt(i-1),EulerY(:,i-1));
end
EulerX=EulerY(1,:); %取x
%%(2)龙格库塔法
RkY=y0;
for i=2:N
k1=f(tt(i-1), RkY(:,i-1));
k2=f(tt(i-1)+dt/2, RkY(:,i-1)+k1*dt/2);
k3=f(tt(i-1)+dt/2, RkY(:,i-1)+k2*dt/2);
k4=f(tt(i-1)+dt, RkY(:,i-1)+k3*dt);
RkY(:,i)=RkY(:,i-1)+(k1+2*k2+2*k3+k4)*dt/6;
end
RkX=RkY(1,:); %取x
%精确解
syms t
analytic=dsolve('D2x=-x','x(0)=10','Dx(0)=0','t');
rightdata=subs(analytic,t,tt);
if PlotFlag
plot(tt,EulerX,'b-',tt,RkX,'r--',tt,rightdata,'g-.')
legend('Euler','Runge-Kutta','analytic')
end
MaxDiffX=[max(abs(RkX-rightdata)),max(abs(EulerX-rightdata))];
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
所有题,都得你自己调步长。
输入:
DiffEulerRk4(0.01,1) %步长取0.01的计算结果,参数为1代表作图,自己得修改步长
%%下面是变化
Error=[];
Dt=[5e-4,1e-3,2e-3,5e-3,0.01,0.05,0.1];
for dt=Dt %几种步长,自行修改
dt %查看dt,步长小,计算量大
Error_1=DiffEulerRk4(dt); %不作图
Error=[Error;Error_1]; %保存欧拉法误差
end
semilogx(Dt,Error)
legend('Euler','RK4')
xlabel('步长')
ylabel('误差')
title('与理论值误差')