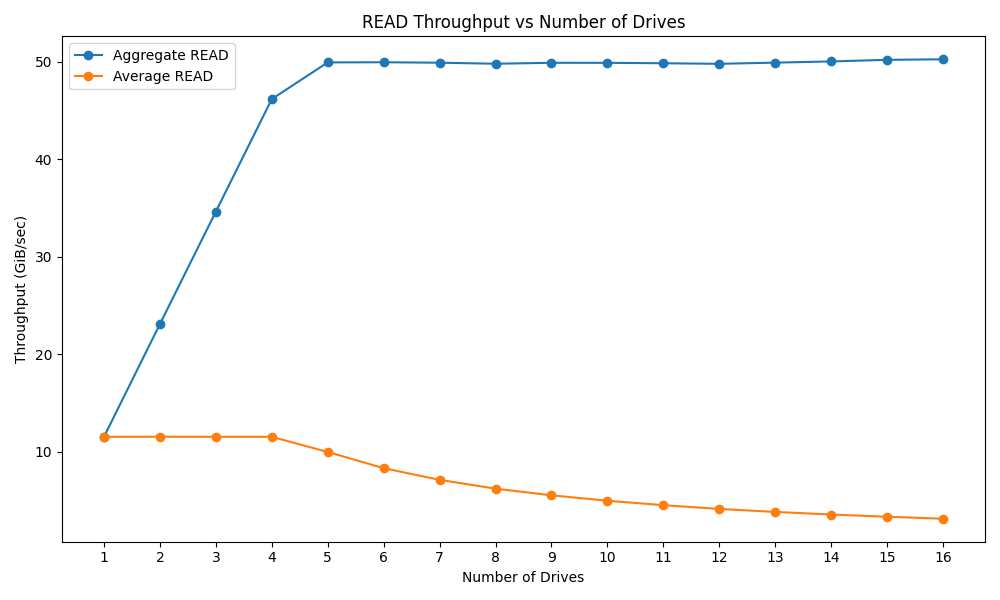
人工智能未来的发展前景怎么样?
人工智能未来的发展前景非常广阔,有四大发展趋势,具体分析如下:
1. 预测行为变化:人工智能工具和平台已经在帮助企业了解客户适应新现实的方式。此前在商业和关系培养方面对数字渠道的采用滞后的机构逐渐认识到这种局面的紧迫性,并在迅速掌握行为分析和个性化等概念。
2.更智能的大数据分析:通过发展我们的能力来把机器学习解决问题技术应用到这些庞大 。我们将更容易发现疫情,举皮跟踪密切接触者,实现更准确的诊断,并通过预测病毒未来可能演化的方式,开发更有效和持久的疫苗接种。
3.自动检测和预防:面部识别比较有争议的一点是,它把重点放在识别个体、而非人群中的模式,因此警方利用这项技术来发现逃避封锁和隔离的人,并追踪人群中出现症状的个体活动。
4.把下一次疫情消灭在萌芽状态:人工智能研究将在未来18个月取得进一步突破,从而提高我们发现和应对病毒暴发危险的能力。
想了解更多有关人工智能未来的发展正岁差前景怎么样的详情,推荐咨询达内教育。达内教育是引领行业的职业教育公司,致力于面向IT互联网行业,培养软件开发工雀搜程师、系统管理员、UI设计师、网络营销工程师、会计等职场人才,拥有强大的师资力量,实战讲师对实战经验倾囊相授,部分讲师曾就职于IBM、微软、Oracle-Sun、华为、亚信等企业,其教研团队更是有独家26大课程体系,助力学生系统化学习,同时还与各大高校进行合作,助力学生职业方向的发展。感兴趣的话点击此处,免费学习一下
计算机发展的四个
计算机的发展表现为四种趋向:巨型化、微型化、网络化和智能化。
1、巨型化。
巨型化是指发展高速度、大存储量和强功能的巨型计算机。这是诸如天文、气象、地质、核反应堆等尖端科学的识而界粉需要,也是记忆巨量的知识信息,以及使计算机具有类似人脑的学习和复杂推理的功能所必需的。巨型机的发展回唱应整切溶树口集中体现了计算机科学技术的发展水平。
2、微型化也响。
微型化就是进一步提高集成度,利用高性能的超大规模集成电路研到见院核只其突制质量更加可靠、性能更加优良、价格更加低廉、整机更加小巧的微型计算机。
3硫纸候、网络化。
网络化能够充分利用计算机的宝贵资源并扩大计算机的使用范围,为用户提供方便、及时、可靠、广泛、灵活的信息服务。
4、智能化。
智能化是指让计算坐看机具有模拟人的感觉和思维过程的能力。智能计算机具有解决问题和逻辑推理的功能,知识处理和知识库管理的功能等等。
当前,世界上凡是有能力研制巨型机的厂商,已大多转向研制并行机或者是研制向量技术与并行技术相结合的向量处理机高度并行化的系统,如vpp500等。总之,超级巨型机系统结构离不开并行处理技术,并行机将逐步取代传统型向量机。大规模并行处理机正值年富力强的壮年时期,技术上已趋于属面奏未随成熟,因而有条件、有基础、有能力担负起攀登万亿次、百万亿次,甚至于更高量级超级计算机的历史使命。万亿次量级的超级计算机有望在今年年内问世。 诚然,并行机在今后的发展史上,在前进的历程中,还会议有许多诸如应用软件不丰富,运算效率不高,高档次代表mpp风格的大系统实际用户还很少等等现实问题。尽管如此,但决不会影响并行处理技术的进一步发展。因而,并行处理技术及其产品大规模并行机系统的竞争是激烈的,前途是光明的,攀登万亿次量级超级计算机的历史使命是能够如期完成的。
地形图四色印刷是哪四色?分别代表什么含义?
什么是四色印刷?
四色印刷,一般指采用黄、品红、青三原色油墨和黑色油墨来复制彩色原稿的种种颜色的印刷工艺。
四色印刷中,C,M,Y,K代表着什么?
C Cyan的简写 中文:蓝色;
M Magenta的简写 中文:洋红;
Y Yellow的简写 中文:黄色;
K Black的简写,中文:黑色。
什么产品必须采用四色印刷工艺?
用彩色摄影的方式拍摄的反映自然界丰富多彩的色彩变化的照片、画家的彩色美术作品或其他包含许多不同的颜色的画面,出于工艺上的要求或是出于经济效益上的考虑,必须经过电子分色机或是彩色桌面系统扫描分色,然后采用四色印刷工艺来复制完成。
采用四色印刷工艺时,如果有较大面积的黑色实地,怎样制版更有利于黑色实地墨色厚实?
采用四色印刷工艺时,为了保证阶调和色彩的正确还原,每一色的墨层厚度都应严格控制。通常在四色印刷中,黑色的实地密度不超过1.8,以这样的密度印刷大面积黑色实地,会缺乏厚实的视觉效果。常用的方法是在大面积黑色实地部分叠印40%左右的青色。
黑色实地叠印少量青色,从色相上看还是黑色,视觉效果却会更加厚实。原本在白纸上只印一色黑时,由于印刷过程中纸毛。纸粉在橡皮布上堆积,或由于其他原因影响到油墨的转移,会使黑色实地上出现白色砂眼,黑白对比非常显眼。如果叠印了青色平网,即使黑色实地上有微少的砂眼,由于露出的不再是白色的纸基,而是青色的网点,相对于黑白对比来说,黑青对比就不那么显眼了,可以使黑底色看起来更加均匀美观。
来源于四色定律
四色定理的诞生过程
世界近代三大数学难题之一(另外两个是费马定理和哥德巴赫猜想)。四色猜想的提出来自英国。1852年,毕业于伦敦大学的弗南西斯·格思里(Francis Guthrie)来到一家科研单位搞地图着色工作时,发现了一种有趣的现象:“看来,每幅地图都可以用四种颜色着色,使得有共同边界的国家着上不同的颜色。”,用数学语言表示,即“将平面任意地细分为不相重迭的区域,每一个区域总可以用1,2,3,4这四个数字之一来标记,而不会使相邻的两个区域得到相同的数字。”这个结论能不能从数学上加以严格证明呢?他和在大学读书的弟弟格里斯决心试一试。兄弟二人为证明这一问题而使用的稿纸已经堆了一大叠,可是研究工作没有进展。
1852年10月23日,他的弟弟就这个问题的证明请教他的老师、著名数学家德·摩尔根,摩尔根也没有能找到解决这个问题的途径,于是写信向自己的好友、著名数学家哈密尔顿爵士请教。哈密尔顿接到摩尔根的信后,对四色问题进行论证。但直到1865年哈密尔顿逝世为止,问题也没有能够解决。
1872年,英国当时最著名的数学家凯利正式向伦敦数学学会提出了这个问题,于是四色猜想成了世界数学界关注的问题。世界上许多一流的数学家都纷纷参加了四色猜想的大会战。1878~1880年两年间,著名的律师兼数学家肯普和泰勒两人分别提交了证明四色猜想的论文,宣布证明了四色定理,大家都认为四色猜想从此也就解决了。
11年后,即1890年,数学家赫伍德以自己的精确计算指出肯普的证明是错误的。不久,泰勒的证明也被人们否定了。后来,越来越多的数学家虽然对此绞尽脑汁,但一无所获。于是,人们开始认识到,这个貌似容易的题目,其实是一个可与费马猜想相媲美的难题:先辈数学大师们的努力,为后世的数学家揭示四色猜想之谜铺平了道路。
进入20世纪以来,科学家们对四色猜想的证明基本上是按照肯普的想法在进行。1913年,伯克霍夫在肯普的基础上引进了一些新技巧,美国数学家富兰克林于1939年证明了22国以下的地图都可以用四色着色。1950年,有人从22国推进到35国。1960年,有人又证明了39国以下的地图可以只用四种颜色着色;随后又推进到了50国。看来这种推进仍然十分缓慢。电子计算机问世以后,由于演算速度迅速提高,加之人机对话的出现,大大加快了对四色猜想证明的进程。1976年,在J. Koch的算法的支持下,美国数学家阿佩尔(Kenneth Appel)与哈肯(Wolfgang Haken)在美国伊利诺斯大学的两台不同的电子计算机上,用了1200个小时,作了100亿判断,终于完成了四色定理的证明。四色猜想的计算机证明,轰动了世界,当时中国科学家也有在研究这原理。它不仅解决了一个历时100多年的难题,而且有可能成为数学史上一系列新思维的起点。
证明方法
证明方法将地图上的无限种可能情况减少为1,936种状态(稍后减少为1,476种),这些状态由计算机一个挨一个的进行检查。这一工作由不同的程序和计算机独立的进行了复检。在1996年,Neil Robertson、Daniel Sanders、Paul Seymour和Robin Thomas使用了一种类似的证明方法,检查了633种特殊的情况。这一新证明也使用了计算机,如果由人工来检查的话是不切实际的。
(不过最近,在一个叫“东陆论坛”的数学性论坛里看见一个推理性的图论证明。)
四色定理的重要
四色定理是第一个主要由计算机证明的理论,这一证明并不被所有的数学家接受,因为它不能由人工直接验证。最终,人们必须对计算机编译的正确性以及运行这一程序的硬件设备充分信任。
缺乏数学应有的规范成为了另一个方面;以至于有人这样评论“一个好的数学证明应当像一首诗——而这纯粹是一本电话簿!”
德·摩尔根:地图四色定理
地图四色定理最先是由一位叫古德里(Francis Guthrie)的英国大学生提出来的。德•摩尔根(A,DeMorgan,1806~1871)1852年10月23日致哈密顿的一封信提供了有关四色定理来源的最原始的记载。他在信中简述了自己证明四色定理的设想与感受。一个多世纪以来,数学家们为证明这条定理绞尽脑汁,所引进的概念与方法刺激了拓扑学与图论的生长、发展。1976年美国数学家阿佩尔(K.Appel)与哈肯(W.Haken)宣告借助电子计算机获得了四色定理的证明,又为用计算机证明数学定理开拓了前景。以下摘录德•摩尔根致哈密顿信的主要部分,译自J. Fauve1 and J.Gray(eds.),The History of Mathematics :A Reader,pp. 597~598。
德·摩尔根致哈密顿的信(1852年10月23日)
我的一位学生今天请我解释一个我过去不知道,现在仍不甚了了的事实。他说如果任意划分一个图形并给各部分着上颜色,使任何具有公共边界的部分颜色不同,那么需要且仅需要四种颜色就够了。下图是需要四种颜色的例子。现在的问题是是否会出现需要五种或更多种颜色的情形。就我目前的理解,若四个不订分割的区域两两具有公共边界线,则其中三个必包围第四个而使其不与任何第五个区域相毗邻。这事实若能成立,那么用四种颜色即可为任何可能的地图着色,使除了在公共点外同种颜色不会。
现画出三个两两具有公共边界的区域ABC,那么似乎不可能再画第四个区域与其他三个区域的每一个都有公共边界,除非它包围了其中一个区域。但要证明这一点却很棘手,我也不能确定问题复杂的程度一对此您的意见如何呢?并且此事如果当真,难道从未有人注意过吗?我的学生说这是在给一幅英国地图着色时提出的猜测。我越想越觉得这是显然的事情。如果您能举出一个简单的反例来,说明我像一头蠢驴,那我只好重蹈史芬克斯的覆辙了……。
如果您认为本词条还有待完善,需要补充新内容或修改错误内容,请 编辑词条