引言
作为一种全新的发电、供电方法,微电网在保障电力供应稳定性、提高电力输送效率等方面发挥了重要作用。为确保微电网能够稳定、持续运行,相关研究人员积极尝试将并行遗传算法引入微电网控制工作中,对最优控制遗传算法变量进行优化,明确并行遗传算法计算流程,基于MATLAB开发环境设计微电网最优控制软件系统,通过这种方式达到“环境最优化”与“经济最优化”双重目标。
1 遗传算法并行性及分类
1.1 遗传算法固有的并行性
实际生活中,不同的物种在同一时刻以“相互独立”的状态进行进化,从宏观层面来看,物种的进化即并行化过程。研究人员将物种的进化过程引入机器人深度学习领域,以遗传算法为核心模拟物种进化过程,利用选择操作模拟物种进化过程中的自然选择,利用变异操作模拟物种进化过程中的基因突变。因此,遗传算法的基础运行逻辑中继承了物种进化的并行性。使用遗传算法处理数据信息时,其数量级为O(n3),这代表遗传算法对N个染色体进行遗传操作,其内部遗传信息的数量级为O(n3),研究人员将其称为“隐含并行性”。
1.2 并行遗传算法分类
1.2.1 全局并行,全局并行作为一种直接并行化模式,主要应用于串行遗传算法领域。全局并行模式的特点在于仅有一个群体,在该群体中,每一个个体可以自由匹配,基于群体适应度调整个体适应度,无论是遗传匹配操作还是遗传选择操作,均具有全局性。该模式下,个体之间相互独立,无须进行信息交互,针对个体的评价主要由主/从进程负责[1]。该模式通常采用同步通信技术,个体适应数据被发送给主进程之后,主进程开始计算个体绝对适应值并根据计算结果进行选择操作,通过这种方式提高遗传算法计算性能。
1.2.2 层次并行遗传算法,研究人员尝试将不同的并行遗传算法的优势集中,提高其搜索以及分析的复杂性,将不同遗传算法进行混合,形成层次并行遗传算法。该遗传算法拥有三种基本的拓扑结构,例如将两种并行遗传算法混合,形成的双层遗传算法(图1)。 
分析图1可以发现,该双层遗传算法的上层结构采用粗粒度(环形拓扑结构),下层则使用细粒度(二维网格拓扑结构),通过这种方式进化子群体。
2 最优控制遗传算法目标函数计算
2.1 最优控制模型
与普通电网相比,微电网系统内部可调节变量较多,例如无功补偿量、分布式电源输出功率等。电力从业人员尝试在不同的微电网运行环境中设置多项目优化模型,但是由于约束条件较为模糊,优化控制结果达不到预期值。因此,研究人员在确保微电网安全稳定运行的前提条件下,从环保性与经济性两方面出发,构建多项目最优控制模型,借助这种方式提高清洁能源利用率[2]。
2.1.1 最优控制目标函数,本次研究中涉及的微电网最优控制目标函数主要分为两部分,即环保性与经济性,其函数表达式为> 
式中:x为待优化变量;G(x)为等式约束;H(x)为不等式约束;fi为第i个被优化目标。
2.1.2 经济性目标函数,该模型中,构成经济性目标函数的指标包括两类:第一类是微电网建设、维护费用,研究人员将这些费用折算到建设期之中;第二类是政府为推动新能源产业发展而给予新能源发电的政策性补贴。
(1)建设期费用> 
式中:CWT为微电网中风力发电设备的建设与运维成本;CPV为微电网中光伏发电设备的建设与运维成本;CFC为燃料电池成本;CMT为微型汽轮机的安装及运维成本;CAD为维持微电网稳定运行的附加成本;常量a、b、c、d分别为风力发电机、光伏电池板、燃料电池、汽轮机的数量。
(2)无功补偿成本>
通常情况下,发电侧无功补偿,运用并联电容器就地补偿模式。因此,研究人员将电容器固定成本折算到建设成本之中。 
式中:CC为并联电容器运行成本;Cf为电容器固定成本;T与η分别为电容器使用寿命及使用频率;QC为分布式电源需要的无功功率总量。
(3)新能源发电补贴>
政府为扶持新能源产业发展,针对新能源发电企业给予政策补贴,通过这种方式降低新能源发电成本,其计算公式如下> 
式中:PWT为一台风力发电机输出功率;SWT为风力发电补贴系数;PPV为一块光伏发电电池板输出功率;SPV为光伏发电补贴系数。
研究人员通过计算建设期费用以及新能源发电补贴具体数据,得出微电网最优控制数据。
2.1.3 环保性目标函数,本次研究中提及的微电网以清洁能源为主(风能、太阳能等),除微型汽轮机工作时会产生少量污染物之外,绝大部分能源达到“零污染物排放”标准。因此,该模型中的环保性目标函数,基于污染物排放处罚对目标函数进行量化,其表达式为> 
式中:n为微电网中的微型汽轮机污染物排放量;MMTi为汽轮机工作时第i种污染物排放总量;PMTi为第i种污染物排放处罚标准。
实际工作中,由于微型汽轮机排放的污染物检测难度较大,因此研究人员假定微型汽轮机以均衡的方式排放污染物,不会受到气压、温度等因素的影响。
2.2 最优控制并行遗传算法
2.2.1 优化定义变量,正式开始计算之前,研究人员对需要优化的变量进行定义,即> 
2.2.2 计算过程,并行遗传算法能够有效处理离散变量问题,同时具备良好的全局寻优能力,因此可以解决混合非线性优化问题,公式(6)中的4个变量即并行遗传算法中的个体基因,其排列结构为{XPT|XWT|WFC|WMT}。
最优控制并行遗传算法适应度计算公式为> 
式中:C为目标函数界限估计值;λi为权重系数,通常情况下,权重系数根据子目标函数重要程度进行确定。
模型构建完毕后,研究人员对该模型进行验证,设M=100,子群体个数为4,即n=4,模型进化迭代次数MAXG=50,其中基因变异概率为0.001,即P=0.001,基因交叉概率为0.8,即Pc=0.8,具体步骤如下[3]>
(1)设置模型中分布式电源参数、目标函数以及约束条件,将微电网负荷参数代入优化控制模型中。
(2)基于二级制编码产生基因初始种群,按照均匀划分原则形成n个子种群。
(3)逐一对子种群中的个体进行函数计算,通过横向对比保留适应度最大的个体。
(4)针对子种群进行不同的遗传操作,包括选择运算、交叉运算以及变异运算,设变异运算概率为Pm,交叉运算概率为Pc,通过计算确定各个子群体的适应值。
(5)通过遗传迁移得到初始种群的下一代群体。本次研究中,工作人员使用单向环连接拓扑结构,将各个子群体中最优个体迁出,使用自适应迁移策略,当子群体连续S=1(迁移数量为1)无法进一步提高适应度时,接受迁移个体。通过这种方式减少个体迁移数量,令不同的子群体分布于模型中的不同区域,提高子群体多样性,通过这种方式提高子群体进化速度。
(6)若种群遗传代数与设定的最大值相同,则计算终止并输出最优解,如果二者不同,则返回步骤(4)重新进行计算,其具体流程如图2所示。 
3 微电网最优控制软件设计
研究人员基于并行遗传算法,以微电网环保目标及经济最优化目标作为优化对象,利用最优控制模型处理多目标优化问题。最优控制软件的主要任务是获取仿真平台传输的参数,并利用最优控制模型寻找多目标任务最优解,将最优解参数返回仿真平台,通过这种方式实现对于微电网的最优控制[4]。
该软件主要由三项功能组成:参数读取、计算最优解、返回参数。同时,设计人员为该系统搭配了一些辅助功能,例如文件退出询问、变量查询以及操作步骤历史记录查询等。研究人员为了能够让用户以更为直观的方式了解最优解计算流程,在该软件中添加了折线图(图3),利用折线图展示子种群进化时每一代适应度最好的种群变化情况。通过这种方式让使用者能够更为深入地了解微电网最优控制方法的形成过程。 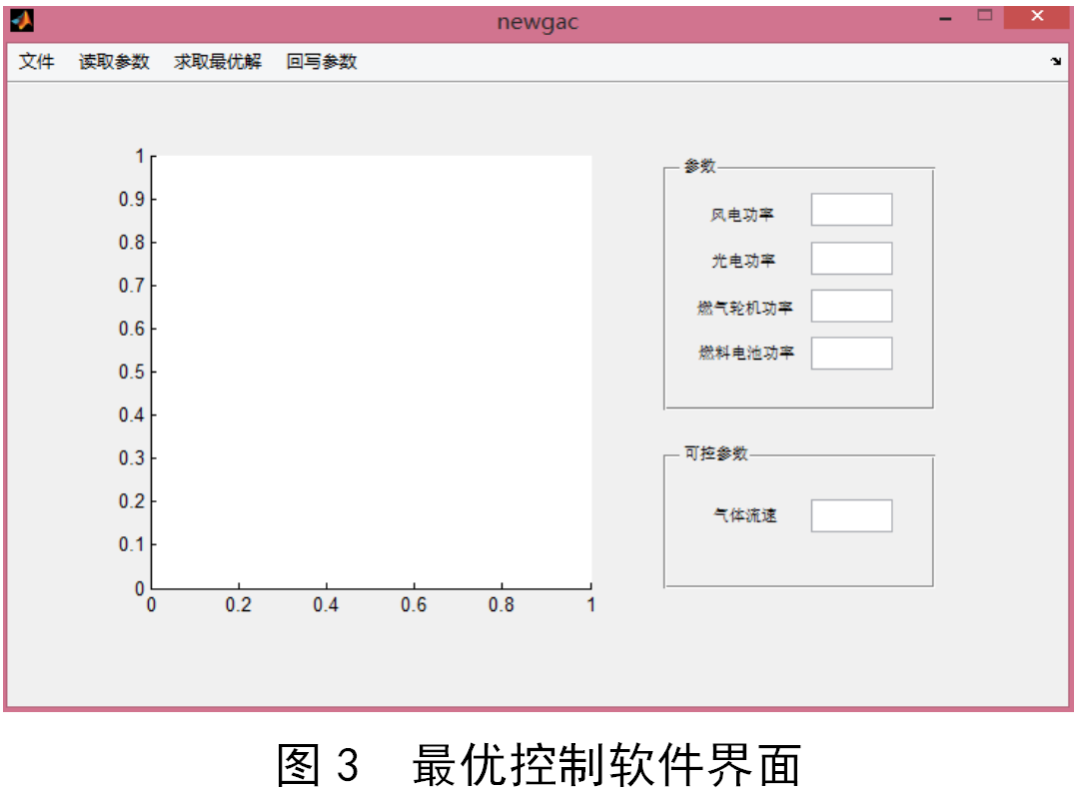
4 结语
为进一步提升微电网控制效率,研究人员引入并行遗传算法,利用并行遗传算法中的多层次并行遗传空间,组建由具有环形拓扑结构的粗粒度以及具有二维网格拓扑结构的细粒度组成的双层遗传算法模型。在此基础上,以微电网经济性与环保性作为目标函数,构建最优控制模型,同时利用MATLAB开发环境设计微电网最优控制软件,为确保微电网稳定运行提供技术支持。
推荐
-
TrendForce集邦咨询: 预估2025年笔电品牌出货成长率将下修至1.4%

TrendForce集邦咨询: 预估2025年笔电品牌出货成长率将下修至1.4%
2025-05-01
-
让英特尔再次伟大,新CEO推动18A提前量产,14A已在路上

让英特尔再次伟大,新CEO推动18A提前量产,14A已在路上
2025-05-01
-
晶振在网通应用增光添彩:中国移动实现数字乡村大升级
晶振在网通应用增光添彩:中国移动实现数字乡村大升级
2025-05-01
-
一文解析电磁场与电磁波的区别

一文解析电磁场与电磁波的区别
2025-05-01
-
黄仁勋中国行的背后,AI芯片暗战与英伟达生存博弈

黄仁勋中国行的背后,AI芯片暗战与英伟达生存博弈
2025-04-19
-
国民技术发布国内首款Arm® Cortex®M7+M4双核异构MCU 面向具身智能机器人

国民技术发布国内首款Arm® Cortex®M7+M4双核异构MCU 面向具身智能机器人
2025-04-19
-
北京机器人传感器公司金钢科技数千万元Pre

北京机器人传感器公司金钢科技数千万元Pre
2025-04-19
-
光子 AI 处理器的核心原理及突破性进展

光子 AI 处理器的核心原理及突破性进展
2025-04-19
-
详解CPU 的大小端模式

详解CPU 的大小端模式
2025-05-01
-
超详细解析!电阻在电路中的作用

超详细解析!电阻在电路中的作用
2025-05-01
最近更新
-
洲明科技再登“中国最具价值品牌500强”

洲明科技再登“中国最具价值品牌500强”
2025-05-21
-
帝奥微AMOLED显示屏电源管理芯片DIO53010简介

帝奥微AMOLED显示屏电源管理芯片DIO53010简介
2025-05-21
-
纳芯微LED线性恒流驱动NSL21610 汽车级40V/单通道具备散热加强功能
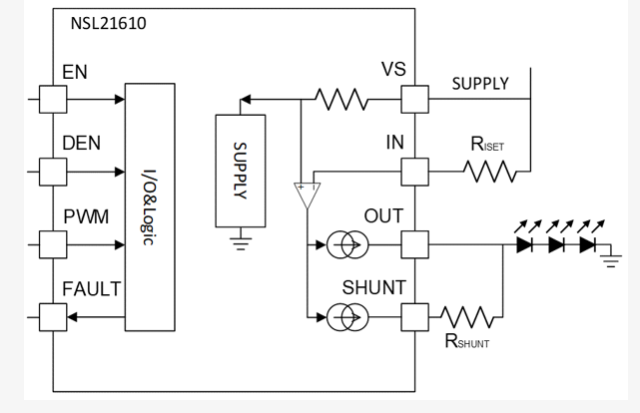
纳芯微LED线性恒流驱动NSL21610 汽车级40V/单通道具备散热加强功能
2025-05-21
-
极海半导体GALT61120汽车前灯LED矩阵控制芯片荣获AEIF 2025 金芯奖

极海半导体GALT61120汽车前灯LED矩阵控制芯片荣获AEIF 2025 金芯奖
2025-05-21
-
使用恩智浦FRDM LCD模组
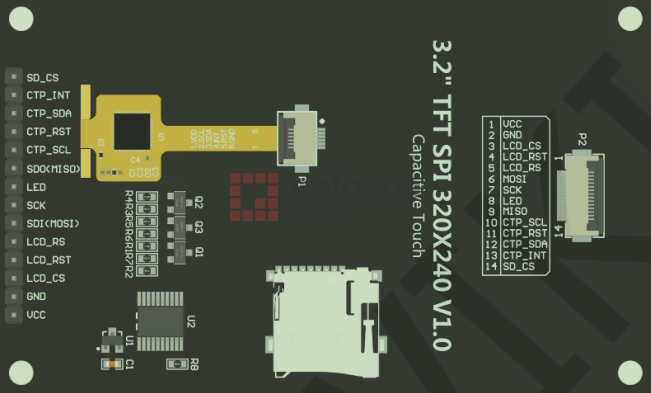
使用恩智浦FRDM LCD模组
2025-05-21
-
【CW32模块使用】1.8寸彩色触摸屏

【CW32模块使用】1.8寸彩色触摸屏
2025-05-21
-
正方科技欧荷18S30AH智能电池在大载重无人机中的应用

正方科技欧荷18S30AH智能电池在大载重无人机中的应用
2025-05-21
-
广和通发布5G模组FG390系列
广和通发布5G模组FG390系列
2025-05-21
-
2025年OBC的新趋势:单级拓扑

2025年OBC的新趋势:单级拓扑
2025-05-21
-
谷歌I/O 2025大会前透露:Android 16接入Gemini,智能手机、XR设备升级

谷歌I/O 2025大会前透露:Android 16接入Gemini,智能手机、XR设备升级
2025-05-21