我们知道,对于OFDM系统,只要不发生载波间扰(ICI),即能够保持子波之间的正交性,就能将每一个子载波看做独立的信道。
这种正交性使得接收信号的每个子载波分量可以被表示成发射信号与子载波的信道频率响应的乘积。因此,仅通过估计每个子载波的信道响应就可以恢复发射信号。
总的来说,可以使用发射机和接收机都已知的导频 (Pilot)符号进行信道估计,并且可以利用不同的插值技术来估计导频之间的子载波上的信道响应。
选择 OFDM 系统的信道估计技术时,必须考虑许多系统实现方面的问题,包括性能需求、计算复杂度和信道时变特性。
常用的信道估计方法有LS估计、LS-DFT估计、MMSE估计、OMP估计等。
在多输入多输出正交频分复用(MIMO-OFDM)系统中,相干检测和均衡需要接收端的信道状态信息(CSI)。然而,在真实的无线环境中,CSI是未知的。因此,信道估计在MIMO-OFDM系统中至关重要。
为简便起见,一般将导频辅助MIMO-OFDM信道估计分解为多个SISO-OFDM信道的同时估计。为了获得更好的信道估计性能,当第i个天线发送导频符号时,所有其他天线必须保持静默。
其中,
是导频位置的集合。
本文考虑了一个具有两个发射天线和两个接收天线的MIMO系统,并利用带有QR分解的OMP算法对MIMO-OFDM信道进行了估计。
OMP算法
设为信道系数的估计值。为非零信道系数的指示集合,为残差,并且,为是测量矩阵的列,是迭代次数。步骤如下。
算法1:OMP算法
Step1:初始化,Step2:通过选择与残差,Step3: 将新选择的索引与索引做并集,Step4:对做QR分解,Step5:计算新的残差,Step6:如果,回到Step2。
Step7: 用反代法求解,得到的k个非零系数。OMP以测量矩阵θ和测量向量y作为输入。在第一次迭代中,选择测量矩阵中与测量向量相关性最大的一列,对其进行QR分解。残差被更新并用于下一次迭代。从第二次迭代开始,选择与残差相关性最大的测量矩阵的列。最后经过K次迭代得到θ的正确列集。在θ上进行QR分解,得到最终的Q和R,然后使用Q, R和y作为反代入的输入得到。QR分解使用改进的Gram-Schmidt正交化进行。
算法2:QR分解
Step1:设,Step2:对,进行循环,Step3:对,进行循环,end for,end for,算法3:回代法
令,Step1:设,且,Step2:对,进行循环,MIMO-OFDM信道估计以2 × 2 MIMO-OFDM信道估计为例,该信道估计分解为4个SISO-OFDM信道,,,和,同时进行估计。
下列MIMO-OFDM系统的仿真参数为:,发射机数量(NT) = 2,接收器数量(NR) = 2,FFT点数量(N_fft) = 512;
每个发射天线导频数(N_P) = 128;
循环前缀长度(N_g) = 64;
信道抽头数(L) = 64;
非零信道系数数(S) = 16;
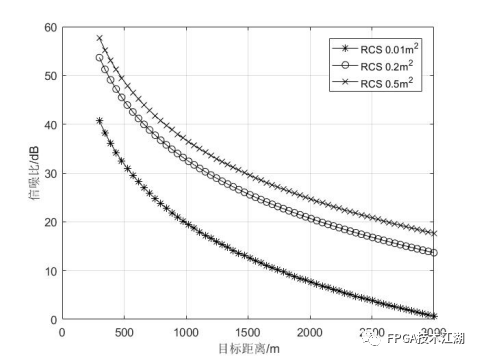
使用的调制方式:16-QAM,编写并执行下面的MATLAB程来估计2×2 MIMO-OFDM信道。2×2 MIMO-OFDM信道估计的Eb/N0与归一化均方误差(NMSE)如图所示。 
从图中可以看出,2 × 2 MIMO-OFDM信道估计,OMP算法性能上优于LS估计。当然若从硬件实现角度看,则OMP算法复杂度更高,耗时更长。
注意,在实际通信系统中,需要根据实际应用场景的信道环境,设计所需的波形,选择合适的信道估计方法。
部分示例代码>
推荐
-
TrendForce集邦咨询: 预估2025年笔电品牌出货成长率将下修至1.4%

TrendForce集邦咨询: 预估2025年笔电品牌出货成长率将下修至1.4%
2025-05-01
-
黄仁勋中国行的背后,AI芯片暗战与英伟达生存博弈

黄仁勋中国行的背后,AI芯片暗战与英伟达生存博弈
2025-04-19
-
让英特尔再次伟大,新CEO推动18A提前量产,14A已在路上

让英特尔再次伟大,新CEO推动18A提前量产,14A已在路上
2025-05-01
-
晶振在网通应用增光添彩:中国移动实现数字乡村大升级
晶振在网通应用增光添彩:中国移动实现数字乡村大升级
2025-05-01
-
国民技术发布国内首款Arm® Cortex®M7+M4双核异构MCU 面向具身智能机器人

国民技术发布国内首款Arm® Cortex®M7+M4双核异构MCU 面向具身智能机器人
2025-04-19
-
北京机器人传感器公司金钢科技数千万元Pre

北京机器人传感器公司金钢科技数千万元Pre
2025-04-19
-
一文解析电磁场与电磁波的区别

一文解析电磁场与电磁波的区别
2025-05-01
-
光子 AI 处理器的核心原理及突破性进展

光子 AI 处理器的核心原理及突破性进展
2025-04-19
-
解决续航、网速痛点,Wi 7 PA杀入AI眼镜

解决续航、网速痛点,Wi 7 PA杀入AI眼镜
2025-04-19
-
15万车型也能有车规SiC!2025年慕展6家厂商新品亮点大揭秘

15万车型也能有车规SiC!2025年慕展6家厂商新品亮点大揭秘
2025-04-19
最近更新
-
芯驰科技与Arteris深化合作

芯驰科技与Arteris深化合作
2025-05-06
-
戴尔PowerEdge R770服务器的性能测试
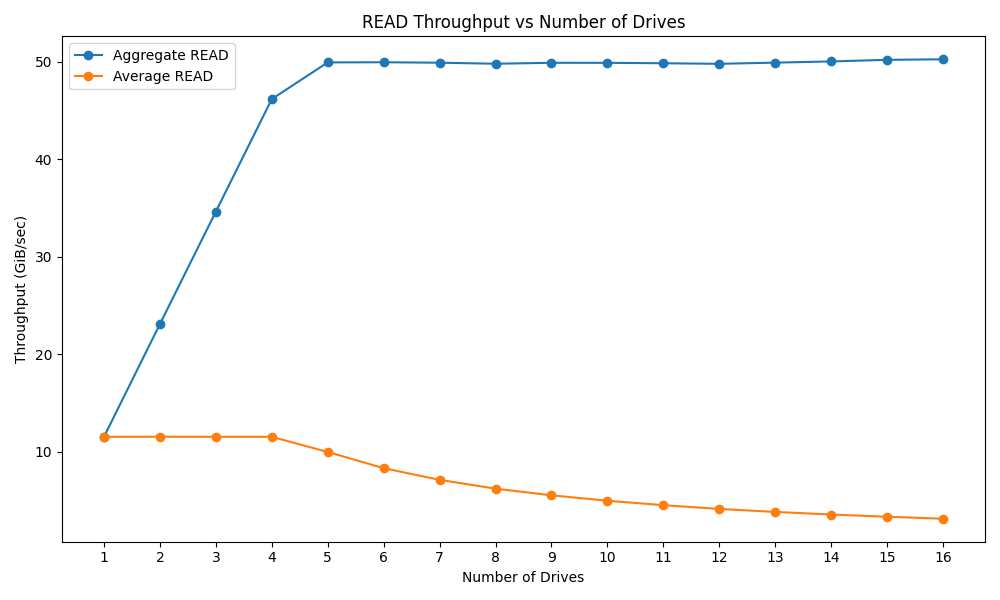
戴尔PowerEdge R770服务器的性能测试
2025-05-06
-
光庭信息与芯驰科技签署战略合作协议

光庭信息与芯驰科技签署战略合作协议
2025-05-06
-
京东方发布2025年第一季度报告

京东方发布2025年第一季度报告
2025-05-06
-
中科曙光DeepAI深算智能引擎全面支持Qwen3

中科曙光DeepAI深算智能引擎全面支持Qwen3
2025-05-06
-
中微爱芯亮相第21届家电电源与智能控制技术研讨会
中微爱芯亮相第21届家电电源与智能控制技术研讨会
2025-05-06
-
中科曙光亮相第八届数字中国建设峰会

中科曙光亮相第八届数字中国建设峰会
2025-05-06
-
RDK全系赋能!点猫科技与地瓜机器人共建具身智能大中小贯通培养闭环要闻

RDK全系赋能!点猫科技与地瓜机器人共建具身智能大中小贯通培养闭环要闻
2025-05-06
-
魔视智能携手德州仪器亮相2025慕尼黑上海电子展

魔视智能携手德州仪器亮相2025慕尼黑上海电子展
2025-05-06
-
曙光存储亮相2025 IT市场年会

曙光存储亮相2025 IT市场年会
2025-05-06