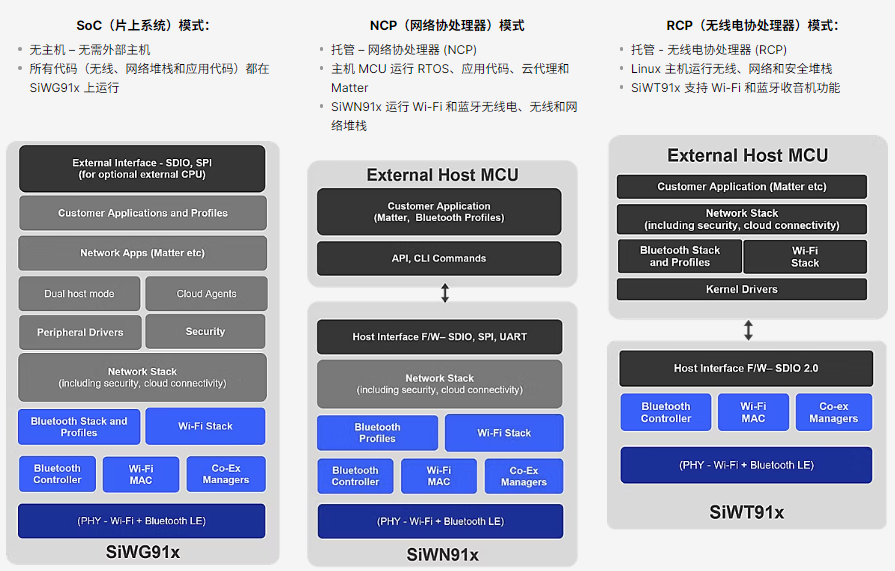
1到6年级学过数有哪些?数的基本概念 自然数数位表 自然数计数单位 小数数位表 小数和分数的基本性质
1、1到6年级学过的数有:小数,分数,自然数,正数,整数(正整数)(负整数),公因数,公倍数,奇数,偶数,负数,乘数,除数,被除数,有理数,无理数。
实数{分 小数(分数)(分 有限小数 和 无限循环小数) 和 整数【分 自然数( 正整数和0的统称) 和 负整数 】}
统计下来就是小数,分数,自然数,正数,整数(正整数)(倒整数),公因数,公倍数,奇数,偶数,负数,乘数,除数,被除数,有理数,无理数 减数 被减数 加数
因数 倍数 百分数 质数 合数。
2、数的基本概念:
自然数
用来表示物体个数的0、1、2、3、4、5、6、7、8、9、10……叫做自然数。
整数
自然数都是整数,整数不都是自然数。
小数
小数是特殊形式的分数。但是不能说小数就是分数。
混小数(带小数)
小数的整数部分不为零的小数叫混小数,也叫带小数。
纯小数
小数的整数部分为零的小数,叫做纯小数。
循环小数
小数部分一个数字或几个数字依次不断地重复出现,这样的小数叫做循环小数。例如:0.333……,1.2470470470……都是循环小数。
纯循环小数
循环节从十分位就开始的循环小数,叫做纯循环小数。例如: , 。
混循环小数
与纯循环小数有唯一的区别:不是从十分位开始循环的循环小数,叫混循环小数。例如, , 。
有限小数
小数的小数部分只有有限个数字的小数(不全为零)叫做有限小数。
无限小数
小数的小数部分有无数个数字(不包含全为零)的小数,叫做无限小数。循环小数都是无限小数,无限小数不一定都是循环小数。例如,圆周率π也是无限小数。
分数
表示把一个“单位1”平均分成若干份,取其中的一份或几份的数,叫做分数。(分成0份在此不讨论)
真分数
分子比分母小的分数叫真分数。
假分数
分子比分母大,或者分子等于分母的分数叫做假分数。(分母、分子为零在此不讨论)
带分数
一个整数(零除外)和一个真分数组合在一起的数,叫做带分数。带分数也是假分数的另一种表示形式,相互之间可以互化。
关于 (n表示自然数)是否是分数
数是由数字和数位组成。
0的意义
0既可以表示“没有”,也可以作为某些数量的界限。如温度等。0是一个完全有确定意义的数。
0是一个数。
0是一个偶数。
0是任何自然数(0除外)的倍数。
0有占位的作用。
0不能作除数。
0是中性数。
约数和倍数
当甲数能被乙数整除时,就说甲数是乙数的倍数,乙数是甲数的约数。这两个概念都是相对而存在。一个自然数,不存在是否倍数与约数。例如:“3是约数”,就是一个错误说法。只能是对3、6、9、……等数而言,是其中某个数的约数。
奇数与偶数
凡是能被2整除的数叫偶数,反之,不能被2整除的数叫奇数。
质数(素数)与合数
一个数的约数只有1和它本身的数叫做质数,也叫素数。反之,一个数的约数除了1和它本身以外,还有其他的约数,这个数就叫合数。
1是否质数
由于1的约数只有1个,所以1既不是质数,也不是合数。
公约数
几个数公有的约数,叫做公约数。
它的个数是有限的,既有最大的,也有最小的。
互质数
两个数的公约数只有1,而没有其他公约数的,这两个数就叫互质数。
质数与互质数
这两个概念没有什么联系。两个质数,不能肯定就是互质数。只有两个不相同的质数,才能肯定是互质数。另外,两个合数既可能是互质数,也可能不是互质数,但不能说两个合数一定不是互质数。
质因数
把一个合数分解成几个质数相乘的形式,这样的质数叫做质因数。
分解质因数
把一个合数分解成几个质数相同的形式,就叫做分解质因数。
公倍数
几个数公有的倍数,叫做公倍数。它的个数是无限的,只有最小的,没有最大的。
最大公约数
几个数公有的约数中,最大的一个就叫做这几个数的最大公约数。
最小公倍数
几个数公有的无限个倍数中,最小的一个,就叫做这几个数的最小公倍数。
能被2整除的判断方法
一个数能否被2整除,只要看这个数的末尾是否有0、2、4、6、8这五个数的其中一个即可。
能被5整除的判断方法
一个数能否被5整除,只要看这个数的末尾是否有0、5这两个数的其中一个即可。
能被3整除的判断方法
一个数能否被3整除,只要看这个数的各个数位上数字的和能否被3整除自然数
用来表示物体个数的0、1、2、3、4、5、6、7、8、9、10……叫做自然数。
整数
自然数都是整数,整数不都是自然数。
小数
小数是特殊形式的分数。但是不能说小数就是分数。
混小数(带小数)
小数的整数部分不为零的小数叫混小数,也叫带小数。
纯小数
小数的整数部分为零的小数,叫做纯小数。
循环小数
小数部分一个数字或几个数字依次不断地重复出现,这样的小数叫做循环小数。例如:0.333……,1.2470470470……都是循环小数。
纯循环小数
循环节从十分位就开始的循环小数,叫做纯循环小数。例如: , 。
混循环小数
与纯循环小数有唯一的区别:不是从十分位开始循环的循环小数,叫混循环小数。例如, , 。
有限小数
小数的小数部分只有有限个数字的小数(不全为零)叫做有限小数。
无限小数
小数的小数部分有无数个数字(不包含全为零)的小数,叫做无限小数。循环小数都是无限小数,无限小数不一定都是循环小数。例如,圆周率π也是无限小数。
分数
表示把一个“单位1”平均分成若干份,取其中的一份或几份的数,叫做分数。(分成0份在此不讨论)
真分数
分子比分母小的分数叫真分数。
假分数
分子比分母大,或者分子等于分母的分数叫做假分数。(分母、分子为零在此不讨论)
带分数
一个整数(零除外)和一个真分数组合在一起的数,叫做带分数。带分数也是假分数的另一种表示形式,相互之间可以互化。
关于 (n表示自然数)是否是分数
数是由数字和数位组成。
0的意义
0既可以表示“没有”,也可以作为某些数量的界限。如温度等。0是一个完全有确定意义的数。
0是一个数。
0是一个偶数。
0是任何自然数(0除外)的倍数。
0有占位的作用。
0不能作除数。
0是中性数。
约数和倍数
当甲数能被乙数整除时,就说甲数是乙数的倍数,乙数是甲数的约数。这两个概念都是相对而存在。一个自然数,不存在是否倍数与约数。例如:“3是约数”,就是一个错误说法。只能是对3、6、9、……等数而言,是其中某个数的约数。
奇数与偶数
凡是能被2整除的数叫偶数,反之,不能被2整除的数叫奇数。
质数(素数)与合数
一个数的约数只有1和它本身的数叫做质数,也叫素数。反之,一个数的约数除了1和它本身以外,还有其他的约数,这个数就叫合数。
1是否质数
由于1的约数只有1个,所以1既不是质数,也不是合数。
公约数
几个数公有的约数,叫做公约数。
它的个数是有限的,既有最大的,也有最小的。
互质数
两个数的公约数只有1,而没有其他公约数的,这两个数就叫互质数。
质数与互质数
这两个概念没有什么联系。两个质数,不能肯定就是互质数。只有两个不相同的质数,才能肯定是互质数。另外,两个合数既可能是互质数,也可能不是互质数,但不能说两个合数一定不是互质数。
质因数
把一个合数分解成几个质数相乘的形式,这样的质数叫做质因数。
分解质因数
把一个合数分解成几个质数相同的形式,就叫做分解质因数。
公倍数
几个数公有的倍数,叫做公倍数。它的个数是无限的,只有最小的,没有最大的。
最大公约数
几个数公有的约数中,最大的一个就叫做这几个数的最大公约数。
最小公倍数
几个数公有的无限个倍数中,最小的一个,就叫做这几个数的最小公倍数。
能被2整除的判断方法
一个数能否被2整除,只要看这个数的末尾是否有0、2、4、6、8这五个数的其中一个即可。
能被5整除的判断方法
一个数能否被5整除,只要看这个数的末尾是否有0、5这两个数的其中一个即可。
能被3整除的判断方法
一个数能否被3整除,只要看这个数的各个数位上数字的和能否被3整除
3、自然数数位表:
由右向左依次为:个位、十位、百位、千位、万位、十万位、百万位、千万位、亿位、十亿位、百亿位、千亿位......
4、自然数计数单位
个、十、百、千 万、十万、百万、千万 亿、十亿、百亿、千亿 、兆、十兆、百兆、千兆 京、十京、百京、千京 垓、十垓、百垓、千垓 秭、十秭、百秭、千秭 穰、十穰、百穰、千穰 沟、十沟、百沟、千沟 涧、十涧、百涧、千涧 正、十正、百正、千正 载、十载、百载、千载 极、十极、百极、千极 恒河沙、十恒河沙、百恒河沙、千恒河沙 阿僧祗、十阿僧祗、百阿僧祗、千阿僧祗 那由他、十那由他、百那由他、千那由他 不可思议、十不可思议、百不可思议、千不可思议 无量、十无量、百无量、千无量 大数、十大数、百大数、千大数 亦可以写作为: 万:10的四次方。 亿:10的八次方。 兆:10的十二次方。 京:10的十六次方。 垓:10的二十次方。 杼:10的二十四次方。 穰:10的二十八次方。 沟:10的三十二次方。 涧:10的三十六次方。 正:10的四十次方。 载:10的四十四次方。 极:10的四十八次方。 恒河沙:10的五十二次方。 阿僧只:10的五十六次方。 那由他:10的六十次方。 不可思议:10的六十四次方。 无量:10的六十八次方。 大数:10的七十二次方
5、小数数位表
十分位 百分位 千分位 万分位......
计数单位是:十分之一 百分之一 千分之一 万分之一......
6、小数和分数的基本性质
分数的基本性质:给分数的分子和分母同时乘或除以相同的数,(零除外)分数的大小不变。
小数的基本性质:在小数的末尾添上0或取掉零,小数的大小不变。
相同点:分数可以化为小数,小数可以化为分数
你好,呵呵、、答案太长了,希望能够帮到你。