1前言
直流变直流电路(DC-DC Converter),也叫斩波电路(DC Chopper)。
能将一种直流电源变换成另一种具有不同输出特性的直流电源的电路,是开关电源的核心。 跟交交变换一样,直流变直流也分为直接直流变流电路和间接直流变流电路。
我们一般按照电路拓扑的不同,将其分为不带隔离变压器的和带隔离变压器的DC-DC变换器。 分类如下:
不带隔离变压器的:降压(Buck)变换器、升压(Boost)变换器、升降压(Buck-Boost)变换器和丘克(Cuk)变换器等。
带隔离变压器的:反激式(Flyback)变换器、正激式(Forward)变换器、推挽式(Push-Pull)变换器和桥式(Bridge)等。
其中,Buck电路和Boost电路是DC-DC变换器最基本的两种拓扑形式。
DC-DC变换器的主要功能是变换直流电压等级,隔离变压器则根据实际情况进行选取,其基本作用是输入输出之间的隔离,也可以进行变压用。
无论哪一种DC-DC变换器,主回路使用的元器件都是功率半导体、电感、电容。 目前使用的开关器件主要有MOSFET、IGBT以及二极管等。
电感和电容则是存储和传递电能的元件。
DC-DC变换器的基本手段是通过控制开关器件的通断,使带有滤波器的负载和直流电源一会儿接通,一会儿断开,从而在负载上得到另一个等级的电压。
其具有功耗小、效率高、体积小、重量轻、电路形式多样等优点,在信息、航天、家电、军事、交通等各个领域得到普遍应用。
可以说DC-DC变换器无处不在了。
接下来,我们就一起慢慢地聊一聊DC-DC的那些事儿~
2降压(Buck)
降压电路,顾名思义,就是将一个原本比较高的电压转换成电压较低的电路,即输出电压小于等于输入电压的单管非隔离直流变换电路。
基本电路拓扑如下:
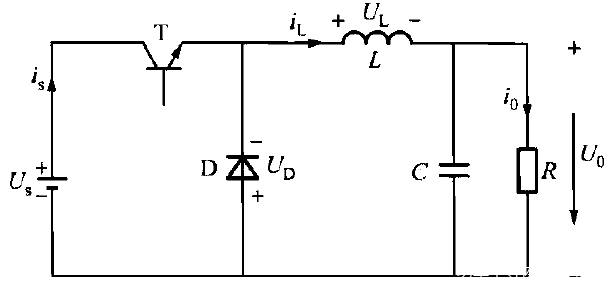
Buck电路的主电路是由开关管T、二极管D、输出滤波电感L和输出滤波电容C构成的,电源是电压源性质,负载则为电流源性质。
为了便于我们分析,这里我们设定了几个前提:
①开关管、二极管均认为是理想器件,即在导通时没有导通压降,截止时没有漏电流(当然,实际情况中,有必要考虑这些因素的);
②电感、电容也认为是理想器件。电感工作在线性区并且未饱和,寄生电阻为零,电容的等效串联电阻(ESR)也为零;
③输出电压中的纹波电压和输出电压的比值很小,可以忽略。
首先,我们定义一个比较重要的参数,占空比。即开关管导通时间ton和开关周期Ts的比值,用Dc表示。
Dc=ton/Ts
根据电感电流是否连续,Buck变换器有三种工作模式——连续导电模式(CCM)、不连续导电模式(DCM)和临界状态(BCM)。电感电流连续是指输出滤波电感L的电流总大于零,电感电流断续是指在开关管关断期间有一段时间流过电感的电流为零。在这两种工作模式之间便是电感电流临界连续状态,即在开关管关断期末,滤波电感的电流刚好降为零。
Buck变换器连续导电模式
(1)
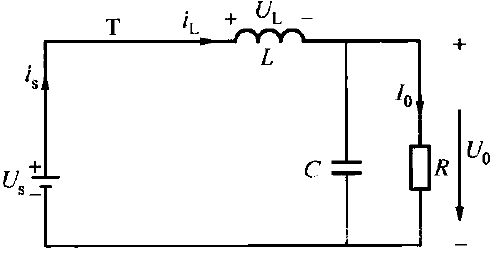
当开关管T导通时,续流二极管反向偏置截止,电容开始重电,直流电压源Us通过电感L向负载传递能量。此时,电感电流iL线性增长,存储的磁场能量也逐步增加。负载R流过电流Io,两端输出电压Uo上正下负。在一个开关周期Ts内开关管T导通的时间为ton。
(2)
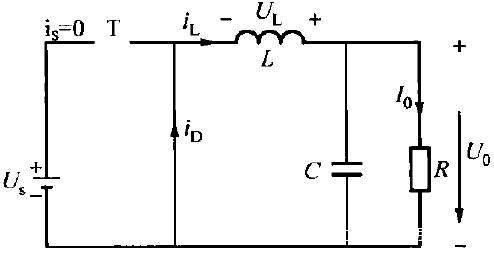
当开关管T关断时,由于电感电流iL不能突变,所以iL通过二极管D续流,电感电流随之逐渐减小,电感上的能量逐步消耗在负载上,iL降低,L上储存的能量减小。电感电流减小时,电感两端的电压UL改变极性,二极管D承受正向偏压而导通,构成了续流回路,负载R两端的电压仍保持上正下负。当iL
在稳态分析中,假定输出端滤波电容很大,我们可以认为输出电压是平直的。同样,由于稳态时,电容的平均电流为零,是因为Buck变换器中电感平均电流等于平均输出电流Io。在连续导电模式下,电感电流不会减小到0,前一个周期结束时刻和下一个周期开始时刻电流是连续的。
工作波形如下图所示
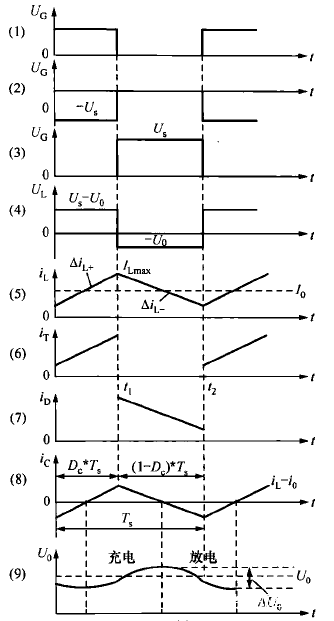
稳态工作的情况下,我们可以得出输入与输出的关系。开关管T导通时,电源电压通过T加到二极管D两端,二极管反向截止。电流流过电感,稳态时输入输出电压保持不变,则电感两端电压极性为左正右负,忽略管压降,则有uL=Us-Uo。由于储能电感的时间常数远大于开关周期Ts,所以在该电压作用下输出滤波电感中的电流iL可以近似认为是线性增长,知道t1时刻,iL达到最大值ILmax。电感电流线性上升的增量为:
![]()
当开关管T关断时,电感两端的电压极性为左负右正,二极管导通续流,忽略管压降则有uL=Uo,同样认为电感中电流iL可近似认为是线性下降,下降的量的绝对值为:
![]()
当电路工作在稳态时,电感电流iL波形必然是周期性重复,那么就有,开关管T导通期间电感中的电流增量等于其截止时电感中电流的减少量,即
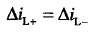
综合上述式子可得
Uo=DcUs
由上式可知,改变输出电压的办法可以调整输入电压Us,也可以改变占空比Dc。在输入电压一定的情况下,改变占空比则可以控制输出平均电压。输出平均电压Uo总是小于输入电压Us。连续导电模式下Buck变换器的电压增益M为
M=Uo/Us=Dc
Buck变换器连续导电模式
当电感较小,负载电阻较小,则负载电路的时间常数较小,或当开关周期Ts较大时,将出现电感电流已下降到0,但新的周期却尚未开始的情况;在新周期里,电感电流从0开始线性增长,工作状态如下所示:
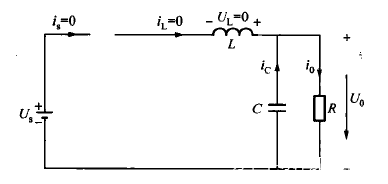
此时一个周期Ts内有3种状态,分为Dc1Ts、Dc2Ts、Dc3Ts。
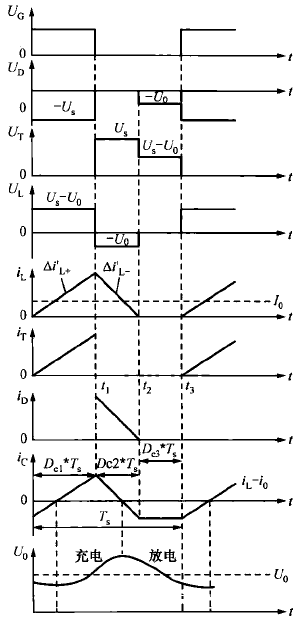
开关管T导通时,Dc1Ts时间从0到t1,电感电流增加量为
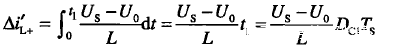
开关管T关断时,Dc2Ts时间电感电流减小量为
根据电感电流增加量等于减小量,可得
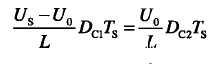
整理可得
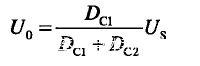
不连续导电模式下,Buck变换器的电压增益M为
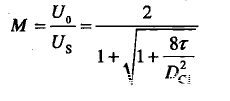
其中,τ=L/(RTs)
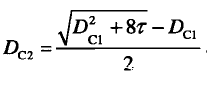
电感电流连续的临界条件
如果在Ts时刻,电感电流iL刚好下降到0,则称之为电感电流连续的临界工作状态,如下图所示
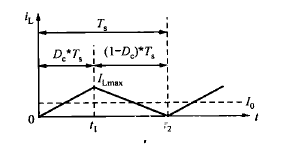
此时负载电流Io和iL之间的关系为
◬iL=2Io
其中,Io=Uo/R
则临界条件下,电感L为
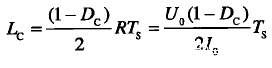
纹波电压◬Uo和电容的计算
流经电容的电流ic=iL-Io对电容充电产生的电压◬Uo称为纹波电压,纹波电压的可以由下式计算
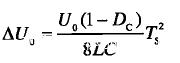
那么,我们可以根据纹波电压的要求和其他参数,求得电容的大小
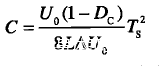
从上面分析可知,电感值和电路中的很多参数有关系,如占空比、负载、开关频率,电容值则跟输出电压、纹波电压、电感值、开关频率、占空比有关系。
开关频率也高,电感和电容的值就越小。
以上便是今天的谈资,直流变换电路中的降压(Buck)电路,主要介绍了三种模式(CCM/DCM/BCM)下的工作原理以及相关计算(当然,分析的前提是相关器件理想化,实际设计中要考虑到器件导通压降等相关参数)。