一、运算微分放大电路
在微分放大器电路中,电容和电阻的位置已经颠倒,现在电抗 XC 连接到反相放大器的输入端,而电阻 Rƒ 正常情况下在运算放大器上形成负反馈元件。
运算放大器电路执行微分的数学运算,即它“产生与输入电压相对于时间的变化率成正比的电压输出”。换句话说,输入电压信号的变化越快或越大,输入电流越大,响应的输出电压变化就越大,变得更像“尖峰”形状。
与积分器电路一样,我们有一个电阻和电容在运算放大器上形成一个RC 网络,电容的电抗 ( Xc ) 在运算放大器微分器 的性能中起着重要作用。
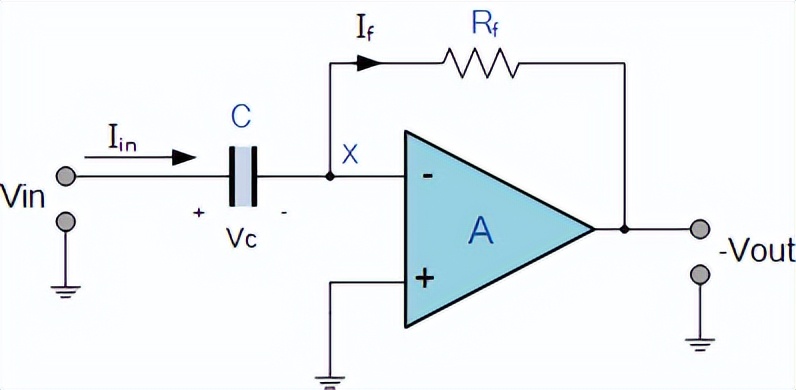
运算微分放大器
如果输入是直流信号,则该电容会完全阻止它,并且 Vout不需要做任何事情来驱动反相输入等于同相输入。因此,任何输入直流信号都不会对 Vout
产生任何影响。
当 V in发生变化时,电路就会发挥作用。在时域中,我们通过以下等式对通过电容的电流进行建模:
电容电流公式
随着电压 V in
的变化,我们得到一个通过电容的电流,该电流开始改变反相输入端的电压。随着反相输入上的电压开始变化,运算放大器输出立即发生变化,既使电流流过某处,又将反相输入保持在
0V。具体来说,随着输入电压升高,输出降低,因此电流可以从反相输入端的 0V
流向输出端的负电压。相反,随着输入电压降低,输出增加,因此现在反向流动的电流可以从输出流到反相输入节点,再到输入。
这是产生微分效应的原因,因为这种响应*仅*在输入电压发生变化时发生——一旦输入电压达到稳定状态并且电流不再流过电容,电压输出将再次降至 0。
二、微分放大电路公式/增益表达式
1、微分放大电路公式
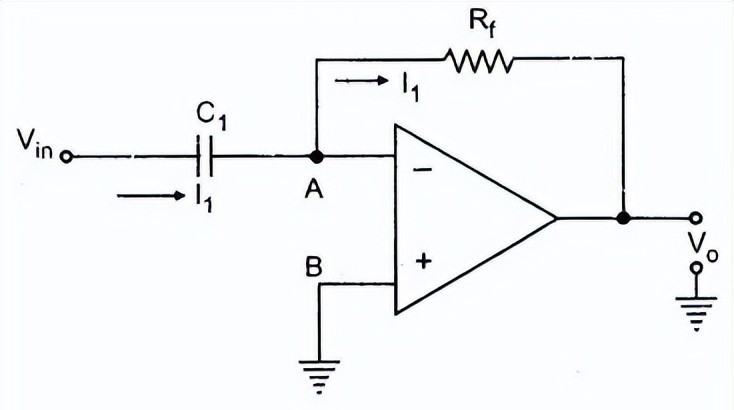
微分放大电路
节点 B 接地,节点 A 也处于地电位,因此 V A = 0。由于运算放大器的输入电流为零,整个电流I 1流过电阻R f。输入端电流:
输入端电流公式
输出端电流:
输出端电流
使两个方程相等,

输入电流和输出电流相等
该等式表明输出是 C1Rf乘以输入的微分,乘积 C1Rf 称为微分器的时间常数。
负号表示输入和输出之间存在 180° 的相移。这种有源微分器的主要优点是微分所需的时间常数小。
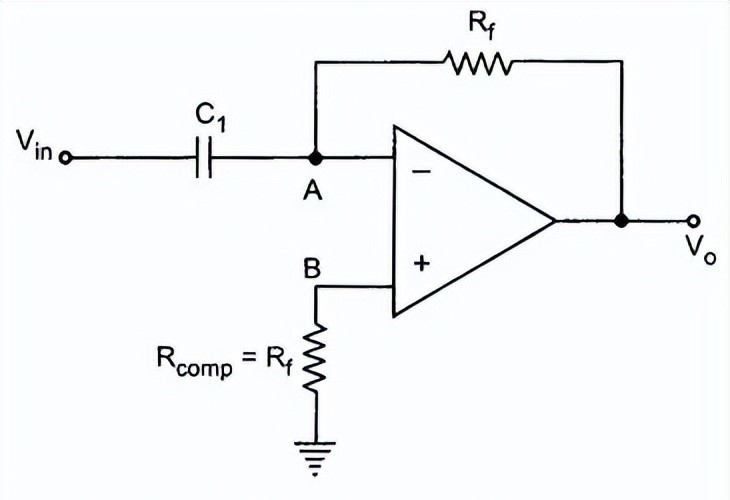
微分放大电路
根据米勒定理,输入节点 A 与地之间的有效电阻变为:
有效电阻公式
A v是运算放大器的增益,它非常大。因此,有效 Rf 变得非常非常小,因此条件 RfC1 ≪ T 在所有频率下都得到满足。
实际上,电阻 Rcomp = R f 连接到同相端以提供偏置补偿。如上图所示:
2、微分放大电路输入和输出波形:
下面研究各种输入信号的输出波形,为了便于理解,假设假设 R f 和 C1的值被选择为具有统一的时间常数 (Rf C1 )。
1)阶跃输入信号:
令输入波形为阶跃型,幅度为 A 个单位。在数学上它表示为:
阶跃输入信号
现在在数学上,微分器的输出是0。

微分放大器电路输出
因为 A 是常数,实际上,阶跃输入需要有限的时间才能从 0 V上升到 A V。由于时间有限,微分器输出不为零,而是在 t = 0
时以尖峰形式出现。由于电路充当反相微分器,负向尖峰或脉冲出现在 t = 0 时,输出保持不变零。
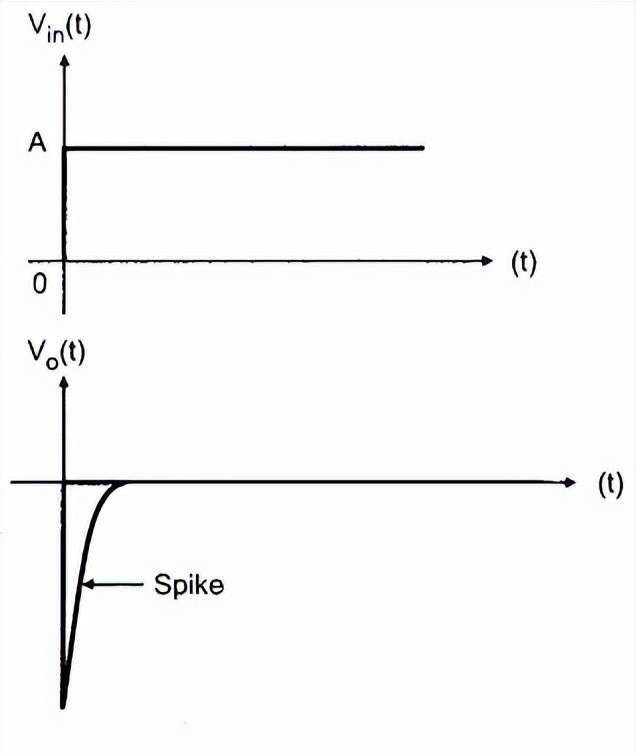
具有阶跃输入的微分器的输入和输出波形
2) 方波输入信号
方波由阶跃组成,即从 t = 0 到 t = T/2 的阶跃为 A 伏特,而从 t = T/2 到 t = T 的阶跃为 -A 伏特,依此类推。
在数学上表示为:
方波输入信号
微分器的行为类似于其对步进输入的行为。对于正向脉冲,输出显示负向脉冲,对于负向输入,输出显示正向脉冲。因此,方波输入的总输出是脉冲串或尖峰的形式。
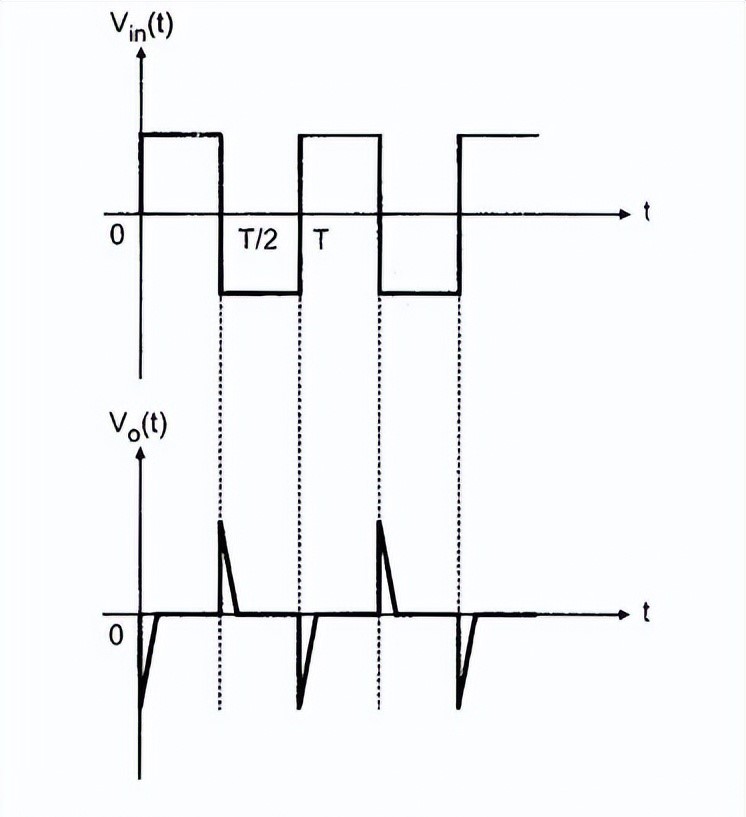
方波输入和输出波形
3) 正弦波输入
让输入波形为频率为 ω 弧度/秒的纯正弦波。在数学上可以表示为,
正弦波输入公式
其中 V m 是正弦波的幅度,T 是波形的周期。
输出的表达式如下所示:
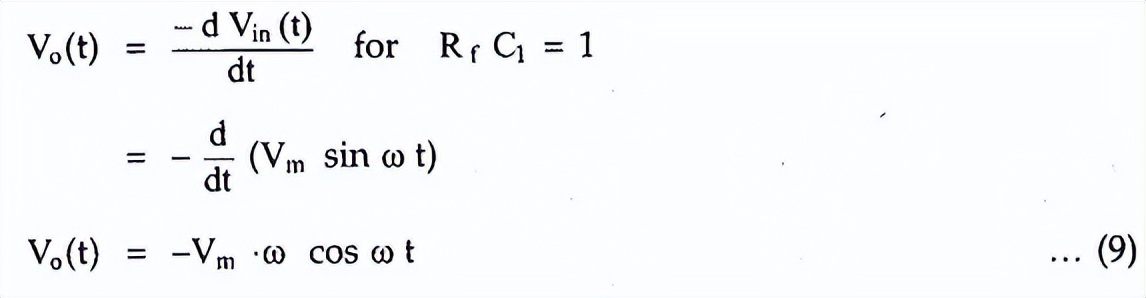
输出表达式
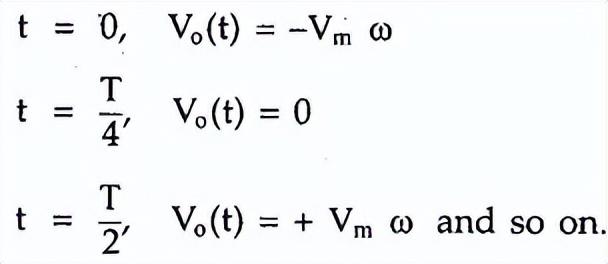
正弦波
因此,对于正弦波输入,微分器的输出是余弦波形。
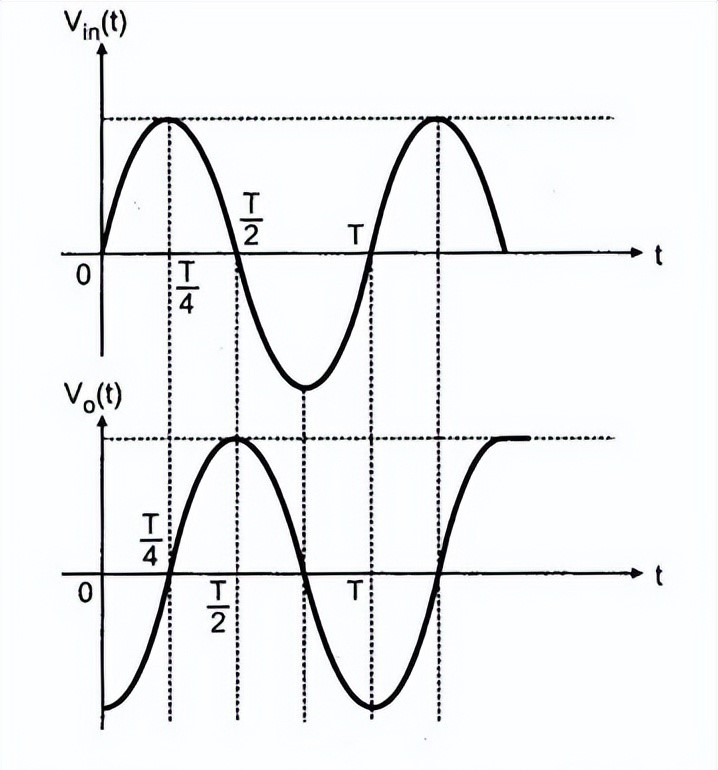
正弦波输入输出波形
下面这个图为微分放大电路输入输出波形图:
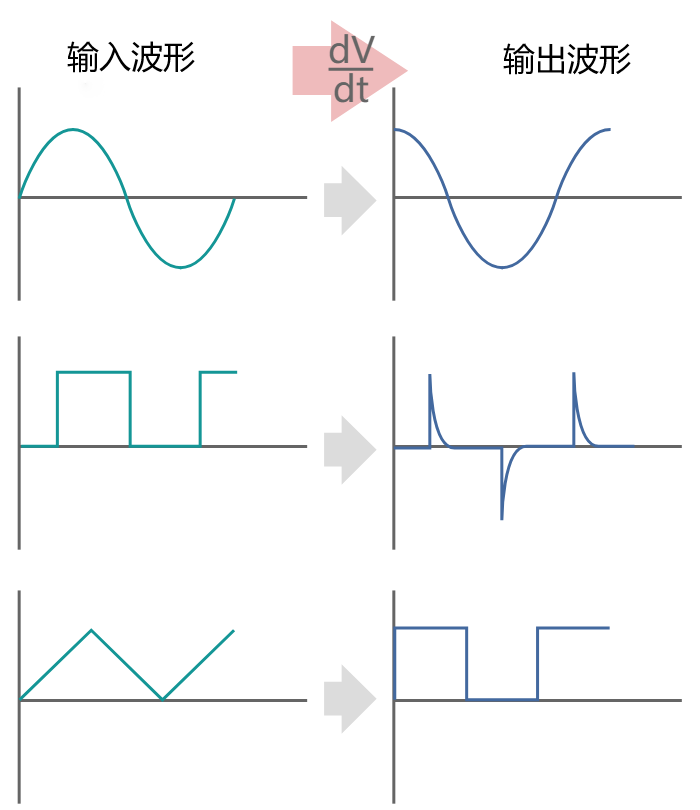
微分放大电路输入输出波形
三、微分放大电路如何设计
为了开发微分电路的电子元件值,必须要确定所需的性能,运算放大器微分器的电压输出:
运算放大器微分器的电压输出
其中:
Vout = 运算放大器微分器的输出电压
Vin = 输入电压
t = 以秒为单位的时间
R = 微分器中的电阻值,以 Ω 为单位
C = 微分器电容器的电容,以法拉为单位 dVin/dt = 电压随时间的变化率。
由于增益以及运算放大器内部的相移,微分器存在噪声问题,有时还存在高频不稳定问题,这些问题可以通过添加一些 HF 滚降来克服。
只需两个额外的电子元件即可实现此目的,用于微分器的运算放大器电路,带有额外的电阻和电容电子元件以确保稳定性。
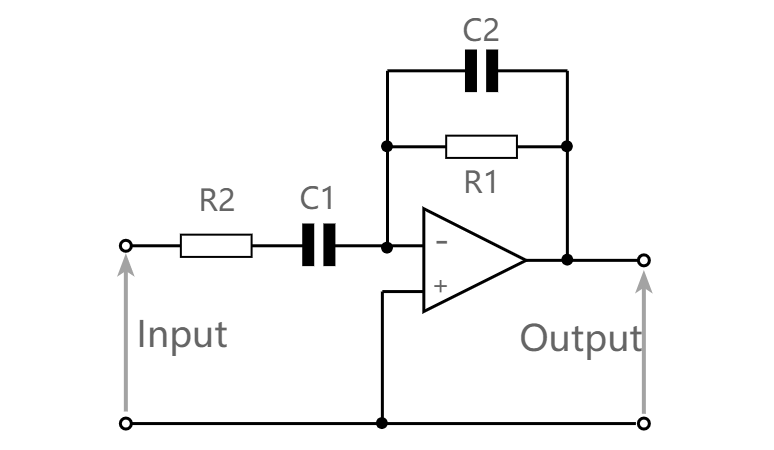
改进后的微分放大电路
电子元件的选择:电容 C2 和电阻 R2 在很大程度上取决于条件 -
噪声水平和所需的微分器带宽。电子元件的较大值以带宽为代价提供了更高的稳定性和噪声降低。
R2 的值可以通过以下等式计算:
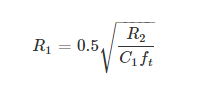
R2 的值计算公式
虽然并不是说一定要用到R2,但可以添加电容 C2 以进一步降低噪声,可以根据下面等式估算出合适的起始值。
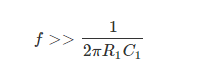
电容C2的确定公式
使用额外的电子元件、C2 和 R2,电路开始成为高频积分器 (f » 1 / 2 π R1 C1)。
这是运算放大器本身的反馈平坦度和整体补偿的结果。
运算放大器微分器设计注意事项
使用运算放大器微分器电路时,需要考虑许多电子电路设计注意事项:
输出随频率上升:
串联电容的一个关键方面是它在更高频率下具有更高的频率响应。微分器输出随频率线性上升,但是在某些阶段并不适用。
因此,在电子电路设计和构建过程中可能需要采取预防措施来解决这个问题。例如,该电路将非常容易受到高频噪声、杂散拾取等的影响。该电路,尤其是其输入必须受到保护,免受杂散拾取的影响,否则可能会中断其运行。
电子元件值限制:
始终最好将电子元件(即电容,尤其是电阻)的值保持在合理的范围内。通常电阻值小于 100kΩ
是最好的,这样运算放大器的输入阻抗应该不会对电路的运行产生影响。
四、微分放大电路设计实例
使用 LM741 运算放大器芯片构建的微分运算放大器电路如下所示:
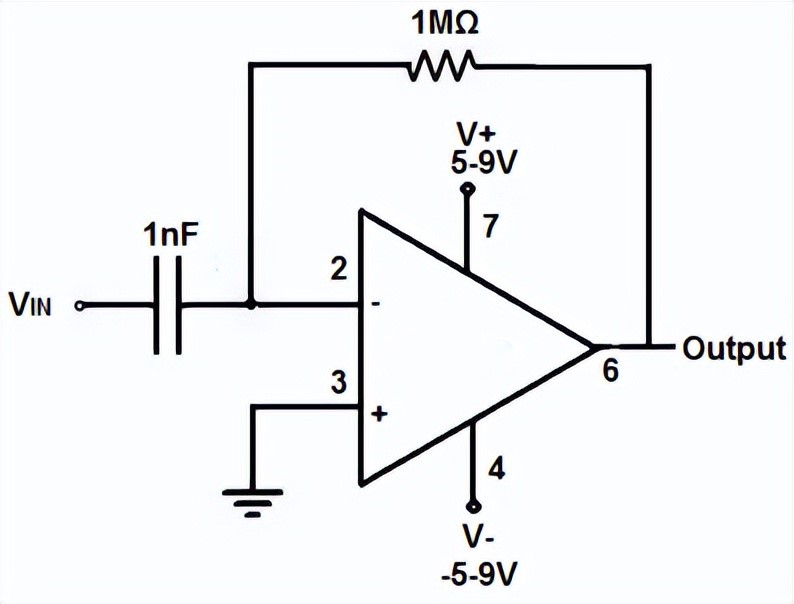
使用 LM741 运算放大器芯片构建的微分运算放大器
下面是上述电路的面包板电路:
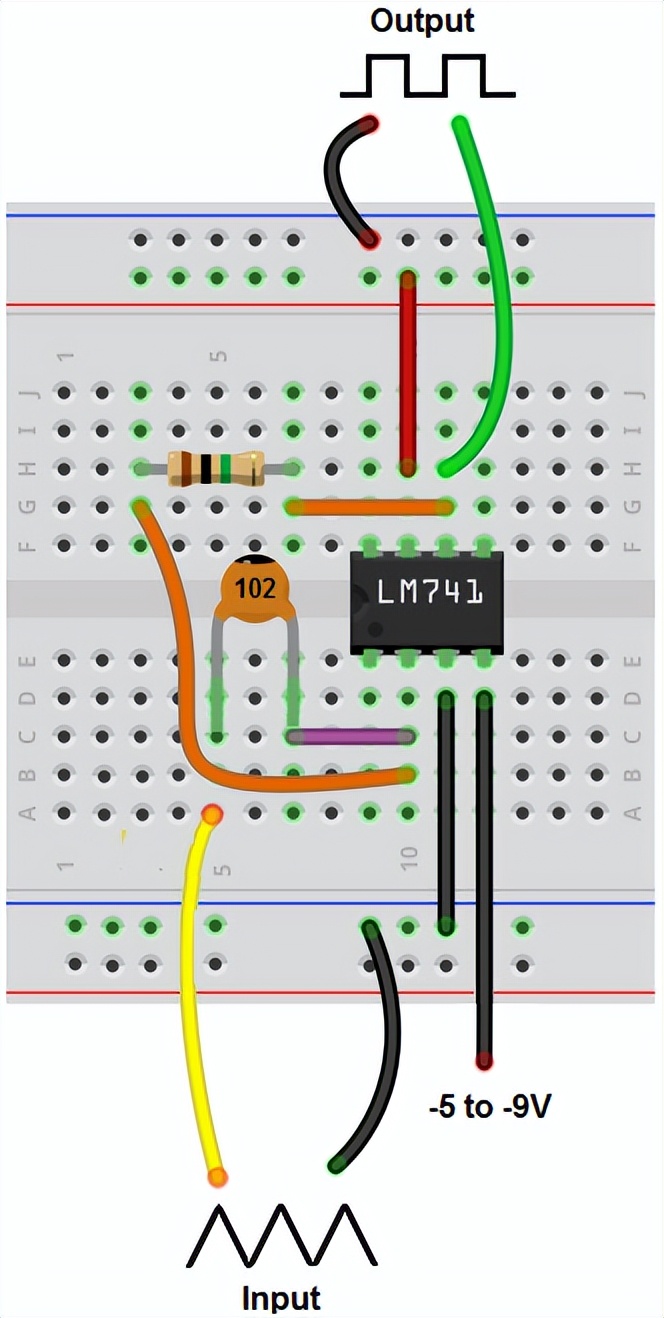
LM741微分放大器面包板电路
因此,当在反相端的输入端有一个电容,而一个电阻的一侧连接到反相端,另一侧连接到输出端时,我们就有了一个微分器电路,所以关于这个电路首先要考虑的是电源要求。
由于我们处理的是交流信号,例如方波、三角波和正弦波,LM741
必须配备双电源。这意味着必须将正电压与负电压一起馈入运算放大器。这样做的原因是可以为运算放大器建立正负直流轨。
现在交流信号,无论是方波、三角波还是正弦波,都可以从这两条轨道摆动。比如说,我们将 +5V 和 -5V 馈入我们的电路,AC 信号现在可以从 +5V
摆动到 -5V。如果我们将 +10V 和 -10V 馈入运算放大器,交流信号现在有更大的摆动空间;它可以从 +10V 摆动到
-10V。如果你看到输出信号出现削波,这意味着电源轨不够高或输入信号太高。
在这个电路中,使用大约 +9V 和 -9V 作为运算放大器的直流电源轨。这对于基本目的来说已经足够了。
+9V 馈入 V+,引脚 7。
-9V 馈入 V-,引脚 4。
这为运算放大器电路建立了电源。引脚 1、5 和 8 未在该电路中使用,因此这些引脚直接悬空。
接下来要考虑的是跨反相端子和运算放大器输出的 RC 网络的值。
在这个电路中,我们使用了一个 1MΩ 电阻和一个 1nF 电容。算一下,这个电路处理的频率非常低,只有几百赫兹。因此该电路将区分接近 100
赫兹范围的信号。它不适用于所有频率。它仅适用于与 RC
网络的值兼容的频率。该电路不适用于超出此范围的频率。所以该电路的输入信号必须低于1KHz左右;否则,电路将不会产生正确的输出。
因此请注意,输入信号的频率必须与用于电阻和电容的值兼容。
对于这个微分电路,如果一个三角波输入电路,输出将是一个方波。因此,如果你将示波器连接到该电路的输出端,以三角波作为输入,你应该在输出端得到一个方波。
五、微分放大电路计算例题
给定图(b)中的输入电压,画出图(a)中电路的输出电压。在 t=0 时,取v o = 0。
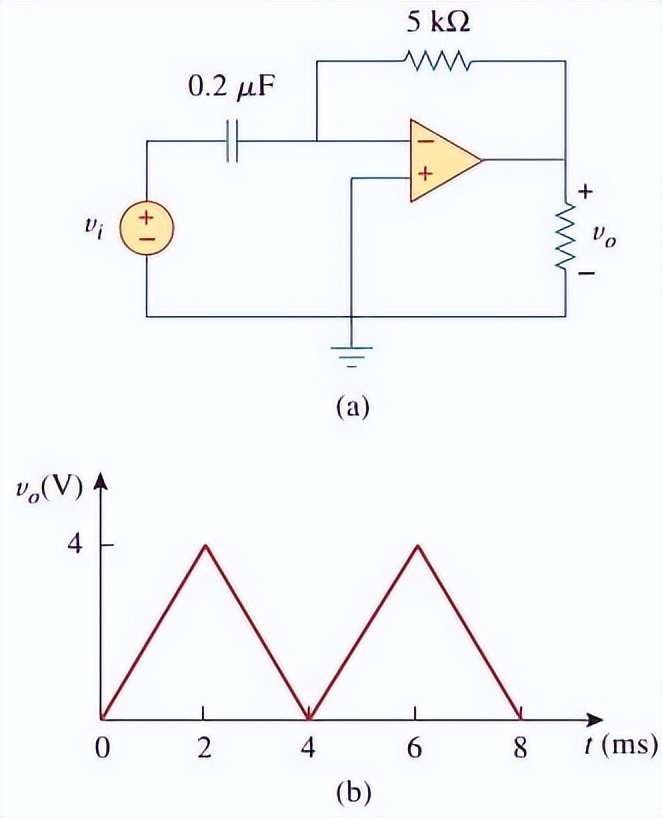
微分放大电路计算示例
这是一个微分器:
![]()
微分器
对于 0 《 t 《 4 ms,我们可以将图 ( b) 中的输入电压表示为:
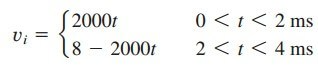
输入电压
这将重复 4 《 t 《 8 毫秒。使用等式(2),输出为:
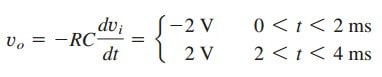
输出
因此,输出波形如下图所示:
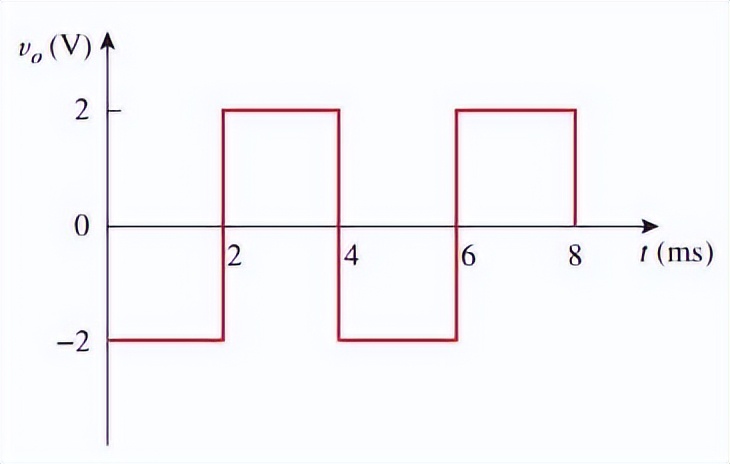
输出波形