OCV(On-Chip Variation)对时序的影响:
• 晶片上的PVT变化,或者说“芯片内变异”(OCV),会引起时序变化。
• 如果在分析和优化过程中未考虑OCV,可能会导致实际的时序违规被遗漏——考虑以下极端示例:
■ 工艺变异本质上是随机的,
• 可能因晶体管而异。
■ 电压和温度变异则是系统性的,
• 并且随着相关单元之间距离的增加而增大。
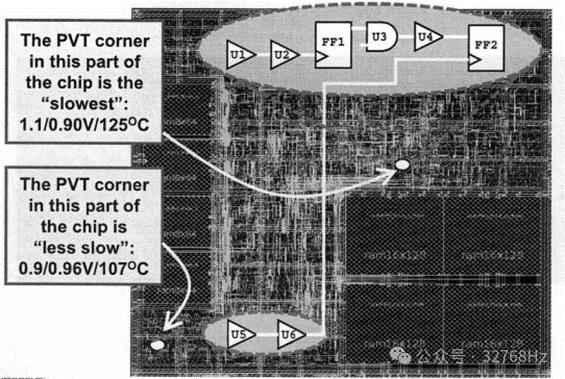
芯片的每个部分并不具有完全相同的PVT参数。晶体管间可能存在随机的工艺变异(P),这会导致延迟差异。温度(T)可能根据布置的单元间不同的功率密度或靠近散热片的程度而在芯片上有所变化。电压(V)也可能根据沿电源网格的IR降而有所不同。电压和温度的变异是系统的——潜在的变异会随距离的增加而增加。术语“芯片内变异”(OCV)用来描述这些随机和系统的变异。
为什么这很重要?
在上面的例子中,如果你正在分析在“最慢”角点下FF1与FF2间的建立时间,并且假设所有单元,包括U5和U6缓冲器,都在同一个“最慢”的PVT角点(1.2/0.9V/125°C)中,你可能会错过一个实际的建立时间违规情况。由于U5和U6缓冲器实际上放置在芯片上一个“不太慢”或更快的区域(1.1/0.96V/107°C),相比于分析所假设的时间,FF1和FF2之间的实际建立时间其实稍微短一些。如果建立时间刚好满足,这是基于所有单元都处于同一最慢角点的乐观假设,那么你将错过一个真实的违规情况!
传统用于建模OCV的时序降额方法
通常每个SLOW或FAST角点只提供一个库
-> 应用估计的降额来模拟PVT变化的综合影响
-
EARLY降额:加快捕捉路径上的建立时间分析,以及保持时间分析中的启动路径
set_timing_derate -late 1.04 -
可以专注于数据或时钟逻辑、网络或单元延迟等
set_timing_derate -early 0.92
对于建立时间检查,启动路径延迟乘以晚期(-late)降额因子(>1),而捕获路径延迟乘以早期(-early)降额因子(<1)。对于保持时间检查,则相反:(启动路径延迟) x (-early因子); (捕获路径延迟) x (-late因子)。
如果没有指定对象列表,默认情况下会对当前设计的单元和网络延迟(但不包括单元检查)进行降额。使用 -cell_delay、-net_delay 和 -cell_check 选项仅对指定的时序弧应用降额;-cell_check 对寄存器的建立/保持和恢复/移除时序弧进行降额(在早期与晚期降额中被视为“启动路径”的一部分)。保持或移除弧的降额是通过(2 - early_factor)来模拟保持/移除时间相应的增加,例如:-early值为0.88模拟了12%的速度提升。由于保持/移除时序弧被视为启动路径的一部分,遵循上述第一段的规则,这些弧应该乘以早期因子0.88,但这会使保持检查变得过于乐观。相反,这些保持检查乘以2-0.88=1.12,这模拟了12%的相应减速,以便进行更保守的时序分析。
时序约束(输入延迟、输出延迟、理想时钟网络延迟)不会进行降额。
-data选项表示降额值仅应用于数据单元。-clock选项表示降额值仅应用于时钟树单元。数据单元与时钟单元在上图中进行了说明。如果不指定任一选项,则降额值将应用于两种单元。
使用report_timing_derate命令验证设置。
使用reset_timing_derate命令恢复到默认的、未经降额的时序设置。
Derate Factor in Timing Report
set_timing_derate -early 0.92
set_timing_derate -late 1.04
report_timing -path full_clock -derate
可以应用增量时序降额:如果设计中已有不想修改的降额设置,但又有必要应用额外的降额时,可以使用以下命令来控制这一操作:
1set_timing_derate -increment ... 2reset_timing_derate -increment ... 3report_timing_derate -increment ...
需要注意的是,write_sdc命令不会写入增量降额信息,而write_script命令则会。
总降额因子会根据所选的降额方法进行计算:
-
简单降额法:
总降额因子 = 基础降额因子 + 增量降额因子 -
AOCVM(Advanced On-Chip Variation Modeling):
总降额因子 = (aocvmGuardband * aocvmDerate) + 增量降额 -
POCVM(Per-Instance On-Chip Variation Modeling):
总降额因子 = (pocvmGuardband * pocvmDistanceDerate) + 增量降额
随机变异的参数化芯片内变异建模(POCV)
• POCV 对单个单元延迟采用了高斯分布模型。
-
每个单元都有一个标称或平均(m)延迟及一个标准差(σ)延迟值(σ也被称为敏感度)。
• 一条路径的累积延迟是通过对每一级延迟分布进行统计叠加来确定的。
统计合并每一级的延迟分布比简单相加每级的最坏情况值更为精确。由此得到的延迟和松弛时间值比通过简单最小-最大相加法计算出的值更加真实,也更少悲观。
POCV输入数据:标准差(σ)- 两种格式

POCV系数的特点是针对每个库单元特定的输入转换和输出负载定义的(σ= C* m):
■ 不依赖于输入转换和输出负载的延迟变化
LVF(Load Variance Function):单元延迟变化量σ(时间单位)是作为每个时序弧的输入转换和输出负载的函数来建模的。
■ 对于更精细的几何尺寸(≤20nm)和低电压,延迟变化强烈依赖于输入斜率和输出负载。