功率因数是电源电路使用有功功率的效率指标,用从0到1的值来表示。其值越接近1,功率因数越高,意味着功率的使用效率越好。交流电功率与功率因数密切相关,如果功率因数低,那么功率波动和损耗就有可能增加。因此,改善功率因数有助于提高电力系统的效率并降低成本。
本文将聚焦“功率因数”,深入探讨其基本概念、实用计算方法以及提高能效的具体手法。
功率因数的定义
功率因数是用来衡量电路效率的指标,用有功功率与视在功率之比来表示。功率因数的取值范围通常是0到1,越接近1,表示效率越高。在直流电路中,功率因数始终为1;在交流电路中,由于线圈和电容的影响,功率因数会发生变化。
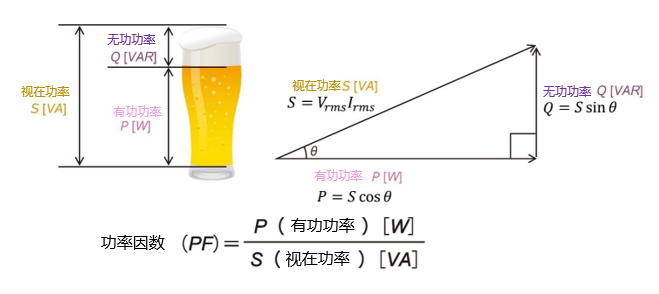
如果将其比作啤酒杯,那么啤酒的液体部分就相当于有功功率,表示实际可以使用的能量,这种能量负责驱动电机或设备。泡沫部分相当于无功功率,是无法饮用的多余能量,但会包含在杯子的总容量(视在功率)中。无功功率主要来自线圈和电容等的有源负载,虽然不消耗能量本身,但会增加电力系统的负载。
啤酒的液体部分与杯子整体容量的比值表示功率因数。功率因数越接近1,也就是杯子里的啤酒越多,泡沫越少,表示能量的使用效率越高。相反,如果功率因数较低,也就是泡沫(无功功率)增多,就意味着系统效率降低,产生了功率损耗。减少这种泡沫部分是提高电力系统效率和降低成本的关键要点。
关于功率因数公式、功率因数的计算、功率因数计算示例的介绍内容,您可点击跳转R课堂查看。
了解功率因数的特性
了解功率因数的特性对于更大程度地提高电力系统的效率而言至关重要。功率因数表示电流和电压之间的相位差;其值越接近1,效率越高。功率因数低会导致无功功率增加,造成电能浪费和设备负荷增大。
功率因数与交流电:通过有功功率和视在功率理解功率因数
要很好地了解功率因数,必须理解它与交流电之间的关系。可以将功率因数视为“功率三角形”。在功率三角形中,三边分别表示有功功率、无功功率和视在功率。
上述示例在功率三角形中表示如下:
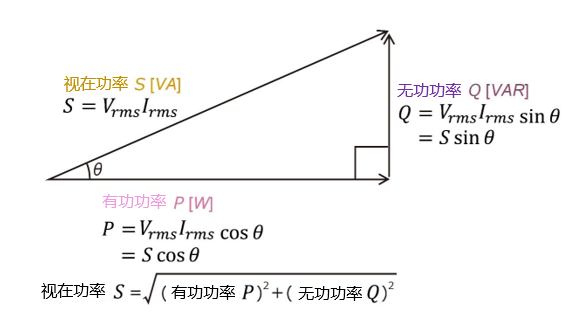
要很好地了解功率因数,理解它与交流电之间的关系至关重要。可以将功率因数视为“功率三角形”。在功率三角形中,三边分别表示有功功率、无功功率以及视在功率。
关于功率三角形、相位差对功率因数的影响、位移功率因数、功率因数1、滞后功率因数、超前功率因数的介绍内容,您可点击跳转R课堂查看。
功率因数校正
功率因数校正是一种能够减少电力系统中电流和电压相位差的技术。这种技术可以提高电能利用效率并降低成本。通过减少无功功率、尽可能地增加有功功率,还可以提高设备的耐用性。例如,改善家用和商用空调以及照明设备的功率因数,有望减少电费。尤其是在工业领域,功率因数校正对于大型用电设施而言非常重要。另外,提高整个供电系统的功率因数,可以减少功率损耗,提高电能传输的效率。
提高功率因数的具体方法
为了提高电路的功率因数而引入的装置和电路被总称为“功率因数校正电路”。
在直流电路中,平均功率可以通过V×I简单地计算出来。然而,在交流电路中情况却有所不同。交流电路中往往有线圈、绕组和变压器等电感元件,电流和电压的相位是存在偏移的。因此,平均功率会小于电流与电压的乘积。这种现象是因为在有电阻和电抗元件(一种电感元件)的电路中,还需要考虑到相位角θ。
因此最好记住:在计算交流电路中的平均功率时,不仅需要考虑电流和电压,还需要考虑相位差。
关于电容电路、有源滤波电路、功率因数补偿装置的介绍内容,您可点击跳转R课堂查看。
功率因数的实际应用示例
改善功率因数与提高电能利用效率息息相关,能够带来更好的经济效益。通过节约能源和延长设备的使用寿命,可以降低应用成本。
工业设备中的功率因数应用示例
工业设备中功率因数的实际应用案例主要与使用电机的工业设备有关。在这类工业设备中,可能存在相位差。例如,在感应电机等负载会波动的设备中,会产生相位差,相位差会影响有功功率的计算。电机在工业设备中的应用非常广泛,提高其效率和功率因数直接关系到提高能源利用效率和降低成本。下面是工业设备中的功率因数应用示例。
- 电机驱动设备
在工业设备中,传送带、电泵、风扇和压缩机等机器都是由电机驱动的。这些电机通常使用诸如感应电机和同步电机等类型的电机。电机在启动时和负载波动时都需要大电流,这必然会给供电系统带来负荷。
如果功率因数低,电机将会产生较多的、额外的无功功率。这种无功功率会给供电系统带来负担,并降低电源效率。另外,供电系统中也会产生功率损耗。
提高工业设备中的功率因数,可以提高供电的稳定性和效率,从而节省电费。改善功率因数的工作有助于工业的可持续发展。
关于家用电器与功率因数、能源供应系统中的功率因数的介绍内容,您可点击跳转R课堂查看。