关于如何为任意特性的PWM选择最佳滤波器元件值的讨论很少,更不用说针对一种设计中所提到的特定PWM(8位,1MHz时钟)。在本文中,我将介绍一种针对任意周期PWM优化这些更简单滤波器的方法。
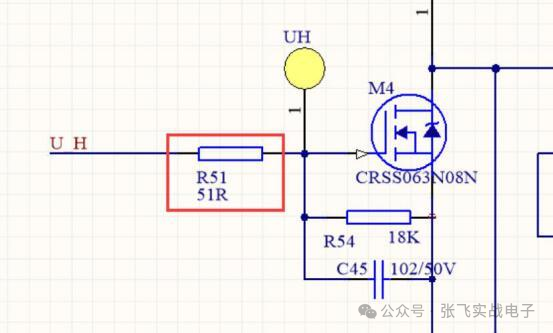
最近EDN美国版上有一系列基于PWM信号“处理器”主题的设计实例发表。这些处理器的目的是最大限度地减少响应PWM占空比变化的建立时间和残余PWM纹波。在许多情况下,更简单的处理器——仅由一个由电阻器和电容器构建的低通滤波器组成——表现良好(图1)。
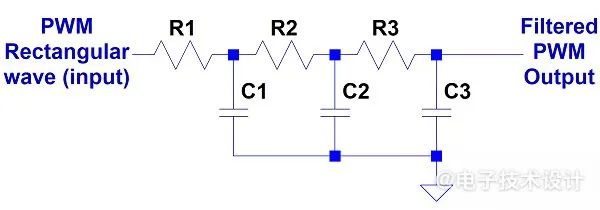
图1:带有低通滤波器的简单PWM处理器,该低通滤波器由电阻器和电容器构成,其结构只能实现实极点。
然而,关于如何为任意特性的PWM选择最佳滤波器元件值的讨论很少,更不用说针对一种设计中所提到的特定PWM(8位,1MHz时钟)。在本文中,我将介绍一种针对任意周期PWM优化这些更简单滤波器的方法。
让我们从一些术语开始:我们将未滤波的PWM描述为具有B个位、占空比为d、周期为T,以及(无单位)输出值为0或1。(警告:如果各位只想为问题找到解决方案,而不想体验推导的快感和数学的痛苦,请跳到本文末尾的“实现解决方案”部分。)
对于具有负的不等极点p1、p2和p3的任何三阶滤波器,单位阶跃的时域响应为:
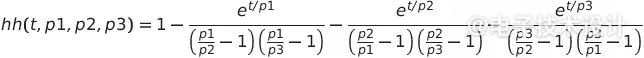
如果有两个或三个极点相等,则响应不同。对于三个极点的情况,它是:
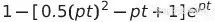
我们的兴趣之一是稳定到1的指定分数F所需的时间(ts)(从d=0到1的满量程PWM转换的最坏情况)。最好是处理幅度稳定误差(ASE)——h(t,p1,p2,p3)=1–hh(t,p1,p2,p3)。ASE在时间t=无穷大时将完全稳定(变为零)。我们可能会想知道是什么样的ts值才能使得h(ts,p1,p2,p3)=F=2-B-1,即PWM的1/2LSB。当然,如果应用能产生更小的最大占空比阶跃,则可以做出其他选择。
我们还对滤波后的PWM纹波的幅度感兴趣。滤波器的频率响应为:
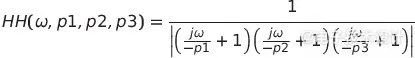
其中j=(√-1),ω是以弧度/秒(rad/s)为单位的频率。
未经滤波的PWM输出可以表示为频率为1/T=ωPWM/(2π)(Hz)整数倍的无限多个正弦曲线的总和。当d=50%且频率为ωPWM时,可产生的最大幅度正弦波具有2/π的峰值幅度。整个PWM信号将通过一个低通滤波器,而使得多次谐波比一次谐波衰减得更多。在这些条件下,一个相当好的低通滤波器的输出,将几乎只包含ωPWM的频率。很明显,过多的纹波和过长的稳定时间同样会让人扫兴。因此,我们试图了解滤波器的ωPWM和ts,以便使ASE和纹波幅度都等于F,也就是说,它们能满足H(ωPWM,p1,p2,p3)=π∙HH(ωPWM,p1,p2,p3)/2=F且F=h(ts,p1,p2,p3)的“标准”。当然,我们还想找到对于给定的F值能够提供最小ts和ωPWM的滤波器。
让我们首先看一下PWM的具体情况,其值为T=28/1MHz=0.000256,其中ωPWM=2π/T=24543。一个明显的起点是具有等值电阻器和电容器的滤波器。对于图1电路,频率响应传递函数为:
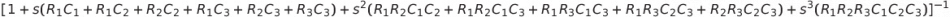
将每个R设置为1Ω,将每个C设置为1F,就可以用多项式求根例程确定满足H()=F=2-8-1的三个极点和ω值:-3.247、-1.555、-0.1981和9.0699。为了在频率ωPWM下获得相同的衰减,可以将极点相乘,将电阻器除以FSF=ωPWM/ω。当然,至少可以说,这些电阻器和1F电容器使用起来不方便。所以,我们可以选择一个阻抗比例因子ZSF,比如10-8来乘以电容,除以电阻。结果为37.0k(选择最接近的标准值)和10n。(运用ZSF对滤波器的响应没有影响。)在已知1Ω/1F滤波器的极点并要求h()=F的情况下,求根例程也为我们提供了ts=32.5s的值。将ts除以FSF,可保持相同的F并使得ts的值等于12.01ms。
当然,没有理由期望相同的R和C所产生的滤波器,在给定的F值下能产生尽可能低的ts和ωPWM。我们应该如何寻找更好的滤波器?我们使用了蒙特卡洛。从上面极点的FSF缩放值开始,选择一组更好的新极点的依据是,它能够减少H( , , ,ωPWM)或h(, , ,ts)的值而不增加另一个的值。我们选择多组随机极点,运行了一个1000万个样本的蒙特卡洛。结果得到了-2290.7、-2238.9和-2218.6处的极点,0.001938
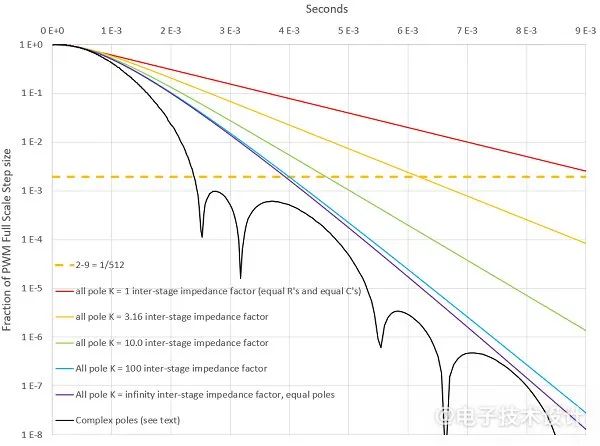
图2:ASE显示了各种滤波器类型的满量程PWM转换与时间的关系。水平线对应于2-9的ASE。
水平虚线处的值为F=2-9。其他每条曲线所对应的滤波器的ASE,其H( , , ,ωPWM)也为F。曲线在滤波器的ASE降至F时与水平线相交。表现最差的是红色曲线,其在K=1的条件下R和C相等。K=√10和10的黄线和绿线更好并且看起来实用,而蓝色K=100滤波器需要K2=10000的阻抗比。紫色K=无穷大的曲线无法实现,对吧?
图1网络的滤波器在驱动阻性负载时会降低精度。最简单的解决方案是在电压跟随器配置中使用运算放大器缓冲它们的输出。使用此运算放大器还有另一大优势:图3中的滤波器配置扩展了可实现的滤波器类型的数量,这样就不仅能包括等极点版本,还能包括性能更好的滤波器——通过反复试验确定的复极点滤波器,其从贝塞尔滤波器的极点开始。“更好”的极点是:-0.84668、-0.786203+j0.725726和-0.786203-j0.725726。可以对该滤波器的R值缩放,使其在ωPWM处的衰减H( , , , )为F。黑色曲线反映了缩放滤波器的性能。为什么会有奇怪的形状?复极点所产生的时域响应包含阻尼振荡。它会在稳定时反复通过零。图中所示的是响应的绝对值。
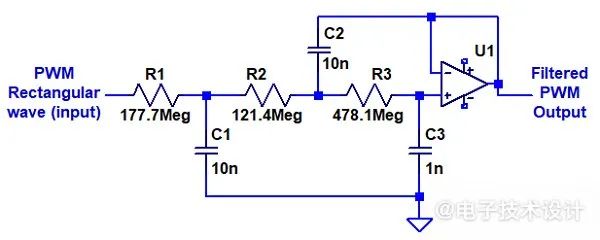
图3:可以实现实极点(部分或全部相同)和复极点的滤波器结构。对于显示的元器件值,表1的复极点部分的每个给定行中的参数值都能得到满足(见正文)。
您可能认为这些图显示了复极点滤波器的先天优势。但它们仅代表F=2-9时能满足“标准”的情况。F的其他值又如何呢?其他值为ωPWM的PWM又如何呢?下面就是答案。PWM具有整数位数,因此仅当N是一组正整数时,考虑F=2-N的值才有意义。对于每个2-N和每个正在考虑的滤波器,我们可以确定出满足“标准”的ω和ts值。知道ω后,就可以对任何所需PWM的ωPWM计算出FSF,而且还可将该FSF用于确定缩放后的ts和滤波器R的值。在具有FSF缩放极点的滤波器中,ωscaled=FSF∙ω,ts-scaled=ts/FSF。因此,无论PWM频率ωPWM为何,ωPWM与FSF缩放的ts的乘积都将保持不变。这个乘积的值越小越好。我们可以对复数同步滤波器的这些乘积进行比较,以确定哪个乘积是每个F值的更好选择。请参阅表1。
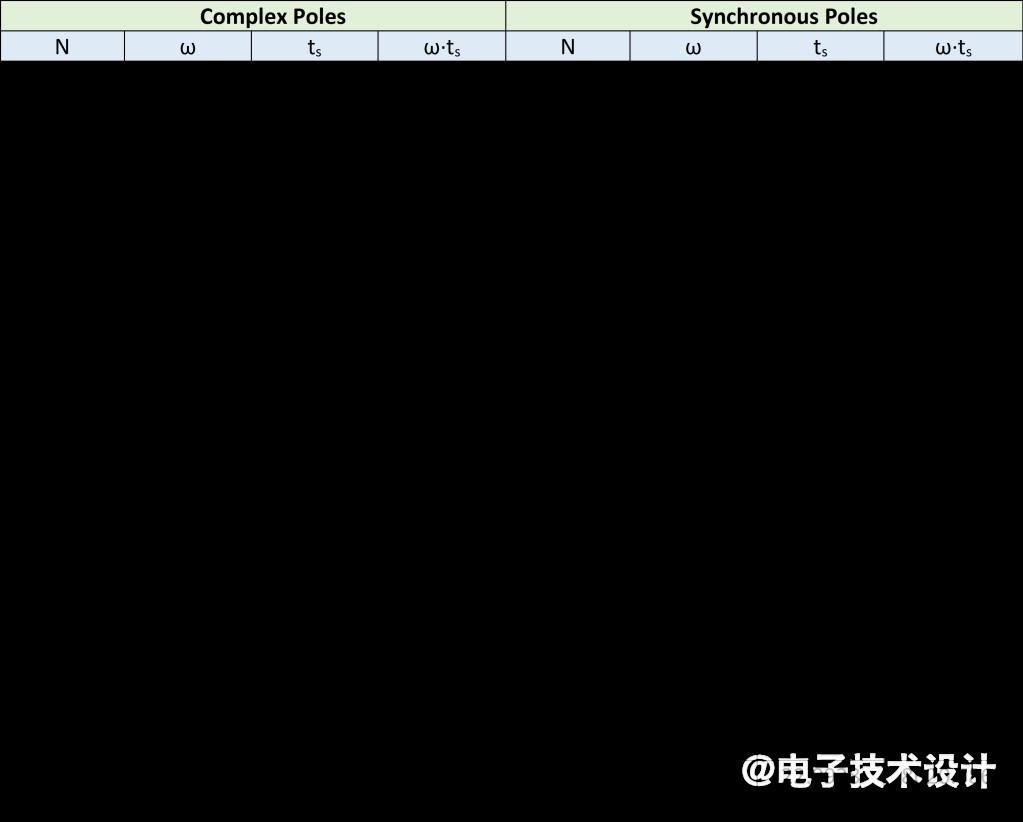
表1:对于各种F=2-N值,复数滤波器和同步滤波器的ω、ts和ω∙ts值。
比较表明,对于每个F,复数滤波器具有更小值的乘积,因此是更好的选择。我们现在可以概括出滤波器设计过程。
实现解决方案
可以用一个具体的例子说明一般问题的解决方案。假设有一个PWM,其中B=8且T=2B/1MHz=0.000256。我们想要获得F=2-9的纹波水平和ASE。图3显示了表1中复数滤波器的滤波器元件值。对于N=9及其F值的情况,滤波器给出的频率为ω=9.1868。但我们希望衰减的频率为ωPWM=2π/T。我们需要将滤波器的电阻器和表格的ts=6.3876除以FSF=ωPCM/ω=2671.7。这样就得到了R1=66.527kΩ、R2=45.445kΩ和R3=178.95kΩ(可以使用最接近的标准值)以及ts=2.39ms。也可以选择通过恒定ZSF来缩放这些电容器和电阻器,将电阻器乘以该值并将电容器除以该值。ZSF操作对滤波器响应没有影响。
应该注意的是,对于N=6或更小的值,同步滤波器具有比复数滤波器更小、更好的ω值,并且对于更大的N值,ω的值几乎相同。尽管如此,复数滤波器仍然是更好的选择——可以使用表中各对ω值之间的数值,将其代入到FSF分母中进行计算。增大ω会使纹波衰减和稳定时间增加。总能找到一个FSF值,使得ω和ts的缩放滤波器值比其他滤波器所提供的值要小。
为任意频率的PWM设计滤波器
本文已经提出了一种使用运算放大器和三对电阻器和电容器来设计用于任意频率和位数的PWM的滤波器的方法。该滤波器可将ASE和峰值纹波限制为F,即用户所选择的2的负整数次幂。还研究了极点间存在各种相互关系的滤波器。所选的复极点滤波器在所考虑的滤波器中具有最小的频率和稳定时间乘积。使用表1和图3,对于任何频率的PWM,可以将滤波器元件缩放到所需的F值。可以对表中所列出的稳定时间运用相同的缩放比例,以计算缩放后的稳定时间。
如果您更喜欢无运算放大器的解决方案,可能需要考虑图1电路的K=10版本。在R1=4.3k和C1=100n的情况下,对于F=2-9,在图2中所看到的绿色曲线的ts约为4.6ms。对于相同的F,该滤波器的ω为15787rad/s。本文没有提供此滤波器的表格,但可以在将不同的FSF运用于滤波器电阻器时在电路仿真器中测试结果。