精简代码逻辑预估，提升阅读体验，快速掌握核心逻辑！

一、开篇寄语

在浩瀚的网络海洋中，我们汇聚于此，共同探索知识的边界，感受思想的碰撞。这里，是智慧的殿堂，是灵感的源泉。让我们携手前行，用文字编织梦想，用思想点亮未来。在这片充满无限可能的领域里，我们将一起领略知识的魅力，共同创造属于我们的精彩篇章。

在这片数字世界的广袤领域中，我们深知，若想FPGA的奔腾之心跳得更加强劲，关键在于确保其逻辑级数轻盈如羽。然而，面对那如星辰大海般浩渺的逻辑工程，一旦代码编织完成，再回首考虑逻辑级数，恐已晚矣。因为在这错综复杂的时序交织中，一处微小的变动都可能掀起连锁反应，迫使整个工程进行痛苦的调整。

因此，要缔造逻辑级数低廉的FPGA设计，我们必须从每个代码细胞开始，便悉心雕琢。为此，我们可以将那些常见的语法模块所蕴含的逻辑级数进行归纳整理。如此，我们不仅能对逻辑级数的疆域有一个大致的感知，更能在优化代码的征途上，找到明确的方向。

当然，这一过程中，Vivado的综合能力将发挥至关重要的作用。逻辑级数的表现与Vivado的综合策略紧密相连。多年来，Vivado经过无数次的迭代与进化，其综合策略已然趋于完善，成为业界的佼佼者。然而，影响逻辑级数的核心要素，依然是代码设计的精湛程度。

请注意，本文的洞察是基于K7系列FPGA得出的智慧结晶。对于其他器件，由于其资源结构各有千秋，我们需重新探寻其独特的逻辑级数之秘。愿每位工程师在FPGA的海洋中，都能驾驭其澎湃之力，创造无限可能。

FPGA设计奥秘：揭秘常见逻辑之美

在FPGA设计的广袤领域中，那些看似繁杂的电路逻辑，实际上都是由一些基础的元素巧妙编织而成。你是否好奇，这些构建FPGA世界的基石究竟是什么？让我们一同揭开它们的神秘面纱。

当谈及FPGA设计的核心逻辑时，不得不提的就是加法器（以及它的变种——减法器和累加器）。它们就像是FPGA中的“数学家”，负责着各种数值的运算。而比较器，则像是一位敏锐的“侦探”，时刻准备着捕捉数值间的差异，为我们提供关键的判断依据。

此外，还有一个不容忽视的元素——条件语句（CASE语句）。它就像是一个智能的“指挥官”，根据预设的条件，灵活地调度着FPGA内部的各项资源，确保整个系统的稳定运行。

当然，FPGA设计中还有许多其他的逻辑元素，如乘法器和存储器等。但它们大多依赖于FPGA内部的专用资源来实现，因此在这里我们暂且不展开讨论。

如果我们能够深入了解这些主要逻辑元素的工作原理，掌握它们的逻辑级数范围，那么对于我们整个FPGA设计的逻辑级数控制将大有裨益。这不仅能够帮助我们优化设计的性能，还能提高设计的稳定性和可靠性。

所以，不妨让我们怀揣着对FPGA设计的热爱与好奇，一起探寻这些逻辑元素的奥秘吧！在FPGA的世界中，每一个逻辑元素都蕴含着无尽的可能与魅力。

探索数学的奥秘：走进神奇的加法器世界

在我们浩瀚的数学海洋中，有一种简单而强大的工具，它就像是数字世界的桥梁，将各种数字紧密地联系在一起，它就是我们熟知的——加法器。

加法器，一个充满魔力的装置，它的功能简单而直接：将两个或多个数字相加，得出它们的总和。然而，这背后所蕴含的数学原理，却让人惊叹不已。每一个加法运算，都是一次思维的跃迁，都是对数学奥秘的一次探索。

想象一下，当你手中的计算器发出“嘀嘀”的声音，屏幕上显示出两个数字相加的结果时，那不仅仅是数字的累加，更是你与数学世界的一次亲密接触。加法器，就像是一个神奇的门户，引领我们走进数学的殿堂，感受数学的魅力。

所以，让我们一起走进这个神奇的加法器世界，感受它带给我们的无限惊喜和可能。让数学不再是枯燥无味的数字游戏，而是充满趣味和挑战的探索之旅。

当我们深入探索数字世界的奥秘时，不得不提及的是那令人着迷的8bit位宽的加法器。它是如何运作的？它的魅力又何在？今天，就让我们一起揭开这层神秘的面纱，探究其内在的奥秘！

在这个浩瀚无垠的数字海洋里，8bit位宽的加法器就像是一艘小巧而灵活的船只，穿梭于二进制数据的波涛之间。它不仅仅是一个简单的计算工具，更是数字世界中的一位重要角色，承载着信息传输和处理的使命。

想象一下，当你输入两个8位的二进制数时，这个加法器就会像一位熟练的数学家一样，迅速而准确地给出它们的和。不仅如此，它还能处理溢出、进位等复杂情况，确保计算的准确性和可靠性。

那么，这个神奇的加法器是如何工作的呢？其实，它的内部结构并不复杂，但却蕴含着深刻的数学原理。通过一系列的逻辑门电路和运算器，它能够将输入的二进制数转化为相应的电信号，并进行逐位的加法运算。最终，通过输出端口，我们就能够得到计算的结果。

在这个数字化时代，8bit位宽的加法器无处不在。无论是在计算机、手机等电子设备中，还是在网络通信、图像处理等领域中，都离不开它的身影。正是这些小巧而强大的加法器，为我们的生活带来了极大的便利和可能性。

让我们共同欣赏这个充满魔力的8bit位宽的加法器吧！在它的陪伴下，我们一起探索数字世界的无限奥秘！

module test(
input [7:0]a_i,
input [7:0]b_i,
output [7:0]sum_o
);


assign sum_o = a_i + b_i;
endmodule

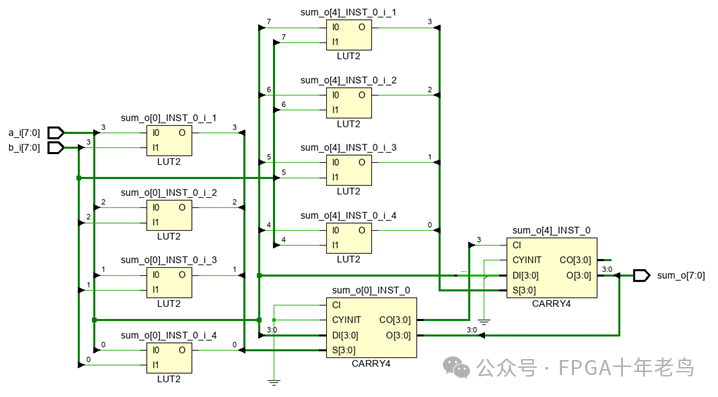
深入探索数字电路的心脏地带，我们不禁被其精妙绝伦的设计所吸引。从细致入微的原理图网表中，我们得以窥见其内在的逻辑层级，那正是令人叹为观止的三级逻辑深度。现在，让我们将目光聚焦在那些默默支撑起这一切的原语上——LUT2和CARRY4。

在数字世界的浩渺星空中，二进制加法器就像一位挥舞魔法的巫师，每一次计算都是对魔法公式的演绎。而这个魔法公式，就是我们所熟知的二进制加法原理，它在这里扮演着至关重要的角色，默默地支撑着整个电路的运算核心。

因此，我们不禁对LUT2和CARRY4这些原语的实现细节产生了浓厚的兴趣。它们是如何巧妙地编织出这个复杂的逻辑网络，又是如何确保每一次计算都能准确无误地执行？让我们一同揭开这些神秘的面纱，探寻数字电路背后的奥秘。

在数字的奇妙世界中，有着一套独特且富有逻辑的语言。这里，我们用一种独特的符号组合来表达各种逻辑关系。瞧，`^` 这个符号，它代表着异或逻辑，如同两个世界在某一刻的碰撞与交融。而 `+` 则代表着或逻辑，就像生活的多样性与丰富性，只要其中之一存在，就充满了可能性。

再来看 `AB`，这不仅仅是两个字母的简单组合，它承载着A与B之间的深厚联系——与逻辑。当A与B同时满足时，它们共同构筑了一个坚实的逻辑基础。

而当我们谈论“和”时，我们用 `O` 这个简洁的符号来表示。它象征着各种元素、各种力量的汇聚，共同创造出一个和谐的整体。

最后，不得不提的是 `CO`，它代表着进位。在数字的海洋中，它如同一个跃升的阶梯，引领我们迈向更高的层次，探索更广阔的领域。

这一切的逻辑与符号，都隐藏在下标 `i` 的每一个bit位数中，如同宇宙中的每一个粒子，都蕴含着无尽的奥秘与可能。让我们一同探索这数字的奥秘，感受逻辑的魅力吧！

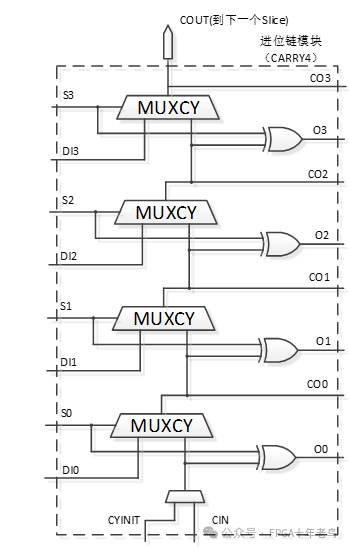
当我们深入探索CARRY4的奥秘时，不禁被其精巧的内部结构所震撼。请允许我为您呈现其内部结构的精华，正如图中所示，每一处细节都凝聚着技术的魅力与匠心独运。让我们一同领略CARRY4的非凡之处吧！

在探索数字世界的奥秘时，有一个重要的基石，那便是二进制加法器。当我们深入剖析其工作原理，理解其内在逻辑，那么，二进制加法器的公式便呼之欲出，其精髓凝聚于下方：

（此处应保留您原有的HTML标签和图片，但您并未提供具体内容，因此我将这部分留白）

在数字电路的世界中，LUT2（查找表2）的存在为复杂运算提供了高效而精准的解决方案。但当我们谈论更高位数的加法运算时，不得不提及的是CARRY4——这款强大的4位二进制加法器。它不仅能在瞬间完成四位数的加法，更能在数字电路中扮演起桥梁的角色。

CARRY4不仅自身功能强大，还能巧妙地与上一级CARRY4进行配合。当上一个CARRY4完成它的使命，产生进位时，CARRY4能够敏锐地捕捉到这一信号，并将其纳入自己的运算中。同时，当CARRY4完成本级的加法运算，它也会毫不吝啬地将当前第4bit的进位输出，传递到下一级的CARRY4中，确保整个加法运算的连续性和准确性。

正是这样的设计，使得CARRY4成为了构建更高位数加法运算的关键组件。无论是8位、16位，还是更高位数的加法，只要通过CARRY4的巧妙串联，都能实现快速而准确的运算。这不仅体现了数字电路设计的巧妙，更彰显了工程师们对于精确和高效的追求。

在数字设计的奥妙世界中，逻辑级数扮演着举足轻重的角色。经过精心调整位宽，我们得出了这些逻辑级数的宝贵数据。亲爱的设计师们，不妨亲自动手实践，深入挖掘这些数据的奥秘，以此来满足您在项目中对逻辑级数的精准估计需求。让我们一起探索，共同追寻数字设计的无限可能！

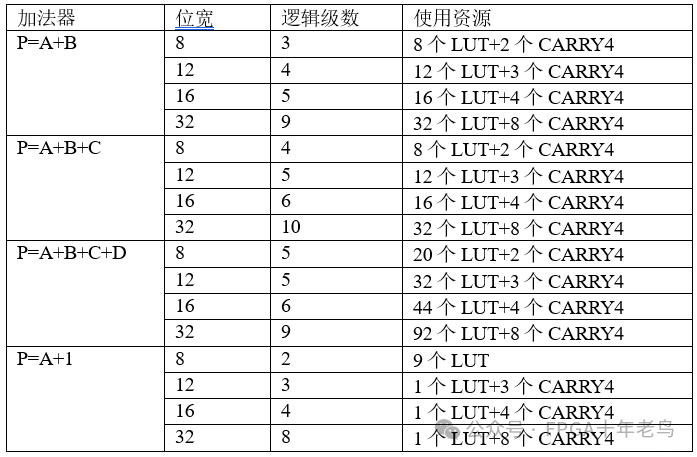
从细致入微的表格数据中，我们窥见了几个引人深思的现象：

每一个数字、每一个百分比，都如同繁星般璀璨，照亮了我们对于未知领域的探索之路。这些现象，不仅是对我们工作的总结，更是对未来发展的指引。

让我们一起深入解读这些现象背后的意义，它们或许能为我们揭示更多的可能性和机会。

在深入了解数字逻辑的奇妙世界中，我们不禁要对Xilinx 7系列芯片中令人瞩目的6输入查找表（LUT6）设计赞叹不已。当我们探讨P=A+B+C与P=A+B之间的逻辑差异时，我们会发现它们在资源使用上有着令人眼前一亮的相似性——两者共享了相同的LUT和CARRY4资源。而在相同的位宽下，P=A+B+C的逻辑级数仅仅增加了1级。

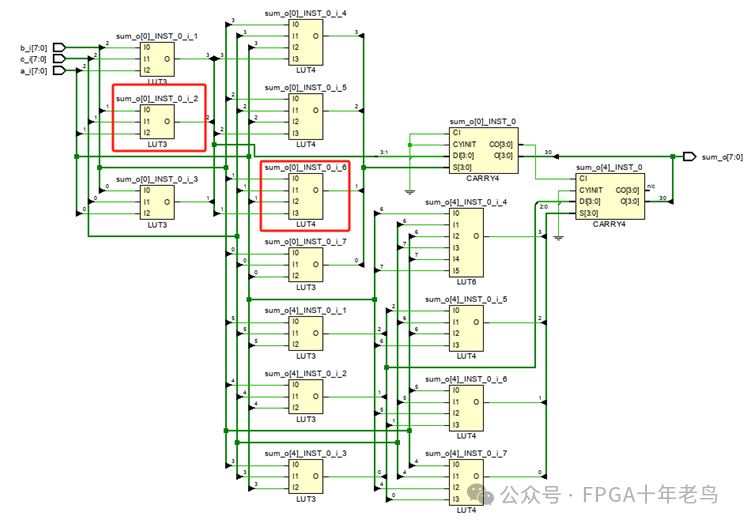
现在，让我们一同揭开图9-3中P=A+B+C综合原理图的神秘面纱。初看之下，你可能会疑惑为何一个看似包含14个LUT的8bit加法操作，在实际资源利用上却仅需8个LUT？这正是LUT6设计的精妙之处。

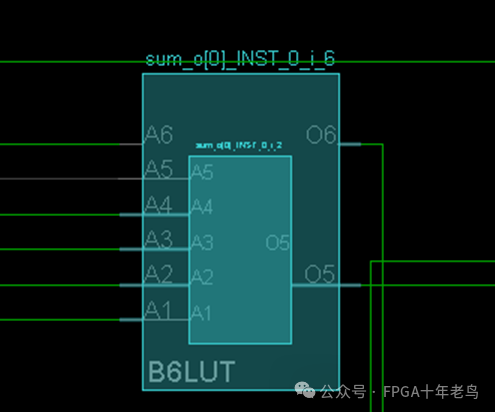
LUT6，这个强大的工具，其内部巧妙地设计为可以拆分成两个LUT5。因此，LUT6拥有两个输出端口，使其能够同时满足两个任意定义的五输入或更少输入的布尔函数。当这两个函数拥有共同的输入，并且LUT6的A6端口被激活时，奇迹就发生了——两个LUT5或更少端口的LUT得以实现。

以图9-3为例，我们可以看到其中的LUT3和LUT4由于拥有相同的输入，被巧妙地综合进了同一个LUT6中。这种设计不仅优化了资源使用，还提升了逻辑运算的效率。

总而言之，Xilinx 7系列芯片的LUT6设计展现了其无与伦比的智能与灵活性，使得数字逻辑设计变得更加高效与精确。

在设计的世界里，每一个决策都如同精心编织的乐章，需要细致地考虑时序与资源的和谐共鸣。当我们面临设计选择时，若时序的紧迫性并未占据主导地位，那么一个简洁而高效的方案便呼之欲出：直接书写P=A+B+C。

这一笔触之下，不仅展现了设计的智慧与美感，更在实际操作中为我们节省了一半以上的逻辑资源。相较于那复杂的两级流水设计（TEMP = A +B、 TEMP = A + C），这一方案如同清泉般纯净，流淌出的是高效与实用的旋律。

在这里，我们不再被繁琐的步骤所束缚，而是用最简单的方式，实现最强大的功能。这便是设计的魅力，用智慧点亮每一个细节，让每一份资源都发挥出最大的价值。

（2）当我们深入探讨P=A+B+C+D与P=A+B+C的32位加法运算时，一个引人注目的现象浮现出来：前者的最高逻辑级数竟然比后者还要小。这种看似颠覆常识的现象，无疑激起了我们内心深处的探索欲望。按照常理，我们可能会认为包含更多项的加法运算（即P=A+B+C+D）应该具有更高的逻辑级数。

然而，现实却给出了不同的答案。在仔细审视这一现象时，我们发现了一个关键线索：尽管前者多了60个LUT（查找表）的使用，但逻辑级数的大小并不只是由代码本身决定。实际上，它与综合工具所选择的实现算法密切相关。这些综合工具在优化资源和时序（逻辑级数）的性能时，会进行精心的权衡和判断。

因此，我们不能仅凭直观感受或简单推理来判断逻辑级数的大小。相反，我们需要深入理解综合工具的工作原理，以及它们如何在各种因素之间找到最佳平衡点。只有这样，我们才能更加准确地把握数字电路设计的精髓，创造出更加高效、稳定的电子系统。

（3）当我们谈论P=A+1型加法或其变种累加器P=P+1时，这不仅仅是一种简单的常数相加操作。尽管从资源消耗的角度来看，它比传统的加法运算更为高效，但随着位宽的增加，其背后的逻辑级数也逐渐展现出其不可忽视的重要性。在数字世界的深处，每一次的累加，都像是精心编排的舞蹈，每一个步骤都精准而有力，确保了数据处理的准确与高效。这种加法方式，就像是一位高效的舞者，在复杂的数据舞台上展现其卓越的才华。