上篇我们了解了运算放大器在使用之前的一些重要注意事项。本篇让我们来了解一下如何将运算放大器在系统设计中使用得恰到好处,让其能力得以充分发挥。
运算放大器的基本应用方式
按照最基本的形式,运算放大器用作同相放大器(图1)和反相放大器(图2)。同相放大器和反相放大器都有负反馈(输出端连接至VIN(-))。闭环增益(ACL)可使用虚拟短路(亦称虚拟接地)概念轻松计算出。
同相放大器的输入阻抗非常高,因为其输入端直接连接至运算放大器。相反,反相放大器的输入阻抗低于同相放大器的输入阻抗,因为VIN(-)和VIN(+)具有相同的电位,因为他们实际上为虚拟短路状态并且R1作为输入阻抗。
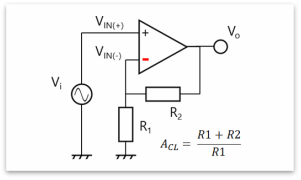
图1:同相放大器
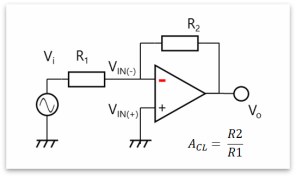
图2:反相放大器
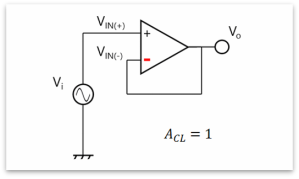
图3:电压跟随器
图3显示了一个电压跟随器。可将电压跟随器视为一个具有无穷大电阻R1且R2为零的同相放大器。由于电压跟随器的增益较低(单位增益,AV=1),因此其带宽较宽。必须要小心的是,电压跟随器容易受第二极点影响。大多数运算放大器可用作单位增益放大器,因为其在充分大于单位增益交越频率(fT)的频率下具有第二极点。而导线或负载电容可能会使其发生振荡。如果给定运算放大器的数据表显示其可在单位增益下使用,则其可用作电压跟随器。
此外,运算放大器具有多种应用,包括差分放大器(减法电路图4)以及加法器(图5)和积分器电路(图6)。
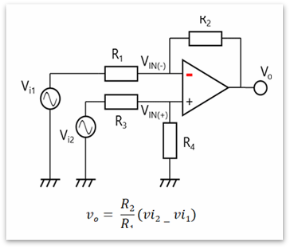
图4:差分放大器(减法电路)
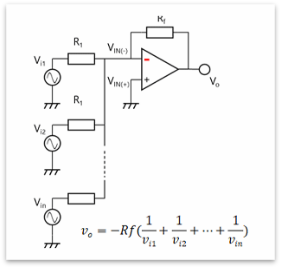
图5:加法电路
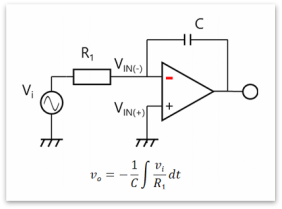
图6:积分电路
虚拟短路
使用虚拟短路(亦称为虚拟接地)的概念,可轻松计算出具有负反馈的运算放大器的闭环增益。虚拟短路概念是指当具有较大开环增益时,无论输入信号如何,具有负反馈的运算放大器的VIN(+)端子和VIN(-)端子其电位几乎相同。
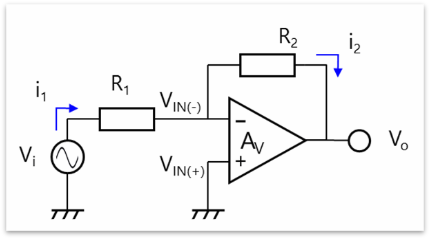
图7:负反馈放大器(反相放大器)
在图7所示的负反馈放大器(反相放大器)情况下,由于输出端与输入端之间的连接方式,输出增加导致输入减少。因此,输出信号介于电源和接地端之间。假设一个反相放大器的输入电压为1此时,运算放大器以100,000的开环增益运行。由于输出电压为3Vpp,故输入电压为3Vpp/100,000=30μVpp。因此,VIN(-)≈VIN(+)。接下来,我们通过简单计算来理解这一点。
假设运算放大器为理想放大器。则会出现以下情况:
1. 无穷大开环增益(AV)
2. 无穷大输入阻抗
3. 零输出阻抗
由于输入阻抗无穷大,流经R1的所有电流(i1)都流经R2。
i1=(Vi–VIN(−))/R1=(VIN(−)-Vo)/R2
(1)由下式得出运算放大器的输出电压:
Vo=AV×(VIN(+)–VIN(−))
(2)根据等式1和等式2,VIN(+)计算如下:
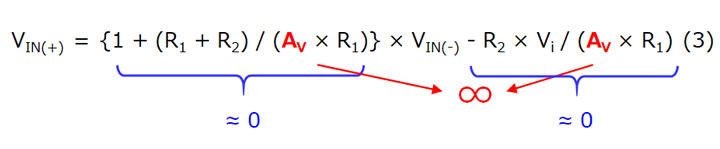
由于输出阻抗为零,我们通过公式3得到VIN(+)=VIN(−)。因此,VIN(−)输入端的电压等于连接至GND的VIN(+)输入端的电压。在这种情况下,VIN(−)输入端的状况即称为虚拟短路。
广义上看,虚拟接地是电路的一个节点,该节点保持在一个稳定的基准电位,不直接连接至电源或接地。在图7的电路中,VIN(-)称为虚拟接地,因为其实际上等于GND。
让我们使用虚拟短路和理想运算放大器计算图8中所示的同相放大器的闭环增益(AV)。我们将输出电压(Vo)表示为Vi的函数。根据虚拟短路概念,VIN(-)=VIN(+)=Vi。
因此,流经R1的电流(i1)计算如下:
I1=VIN(-)/R1=Vi/R1
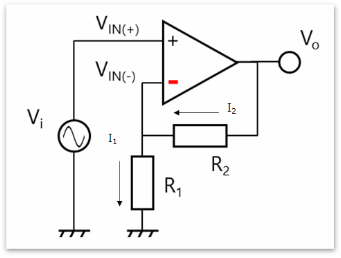
图8:同相放大器
无电流流向运算放大器输入端,因为其具有无穷大阻抗。设流经R2的电流为I2,I1=I2。故R2两端的电压(VR2)为:
VR2=R2×I2=R2×Vi/R1
故Vo计算如下:
Vo=VR1+VR2
=Vi+R2×Vi/R1=Vi×(R1+R2)/R1
AV=Vo/Vi=(R1+R2)/R1
您可轻松得到闭环增益等式。
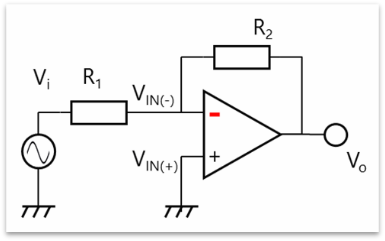
图9:反相放大器
也可用相同方式计算出图9所示的反相放大器的闭环增益(AV)。
VIN(-)=VIN(+)=0V(GND)
I1=V1/R1=I2
Vo=VR2=R2×I2=R2×V1/R1
故闭环增益为:
AV=Vo/Vi=R2/R1
如上所述,可使用虚拟短路和理想运算放大器概念轻松计算出闭环增益。
本篇全面分享了运算放大器的各种使用方式,下一篇我们将和您介绍运算放大器的电气特性。
关于东芝电子元件及存储装置株式会社
东芝电子元件及存储装置株式会社是先进的半导体和存储解决方案的领先供应商,公司累积了半个多世纪的经验和创新,为客户和合作伙伴提供分立半导体、系统LSI和HDD领域的杰出解决方案。
东芝电子元件及存储装置株式会社十分注重与客户的密切协作,旨在促进价值共创,共同开拓新市场,期待为世界各地的人们建设更美好的未来并做出贡献。