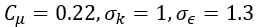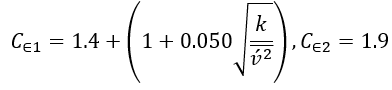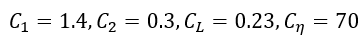本文翻译转载于:Cadence Blog
作者:Gaurav
要点
●提出一种“代码友好”的模型变体,以提高数值稳定性。
●实践表明,如果使用隐式的、逐个方程分离的方法,该变体具有一定优势。这个变体缓解了由壁面边界条件引起的与 Durban 原始模型
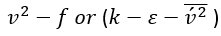
相关的“刚度问题”。
●当雷诺数较高、近壁网格间距极小时,这种作用更加明显。

挖掘 V2-f 湍流模型在复杂流动中的潜力
在高速空气动力学中,利用二阶矩闭合来研究冲击/边界层相互作用的研究很少。究其原因,是雷诺应力方程缺乏明确的二阶扩散项,导致数值稳定性差。(例如,Batten 等,1997;Ha Minh 和 Vandromme,1986;Lien 和 Leschziner,1993)。当所有雷诺应力分量都存储在精确位置时,这个问题会变得更加严重,导致速度与应力解耦和令人头疼的棋盘振荡。
在曲面上设置边界条件较为复杂,这是在数值上实现二阶矩闭合的一个重大挑战。大多数低雷诺数 (Re)二阶矩闭合模型都非常复杂,但只在较为简单的流体场景下进行了验证,例如 Craft 和 Launder(1996)开发的模型。因此,当 y+ 值约为 60 时,需要将高雷诺数模型(Gibson 和 Launder,1978)与标准低雷诺数涡流粘度模型结合起来,以确保湍流仿真中的平滑过渡。
然而,Patel(1985)等人研究的大多数低雷诺数
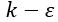
模型都在涡流-粘度表达式中加入了一个特殊的粘性阻尼函数
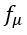
,即
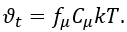
。
阻尼函数修正了涡流-粘度公式在接近固体壁面时不适当的渐近行为。它通常是非线性的,并能引起数值刚度。Durbin(1991)建议,在上述方程中,应使用与流线法向的
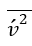
湍流应力,而不是使用 k 来表示壁面的运动阻塞。
因此,
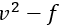
模型无需再使用粘性阻尼函数。
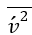
数量是从输运方程推导而来,这是二阶矩闭合理论的简化版。
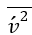
方程中的压力-应变项发挥着至关重要的作用,可在壁面附近重新分配湍流能量,确保正确的湍流水平和恢复各向同性。这是通过辅助椭圆松弛方程实现的,该方程提供了更准确的近壁湍流行为表现。
理解 V2-f 湍流模型的核心原则
Durbin 1995 年的突破:针对精密流体分析,揭开原始 V2-f 模型的秘密。
Boussinesq 近似彻底改变了应力-应变关系,提高了准确度。
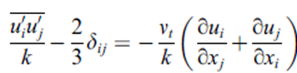
涡粘度由以下公式得出:
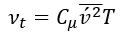
湍流时间由以下公式得出:
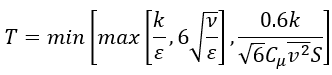
湍流长度尺度由以下公式得出:
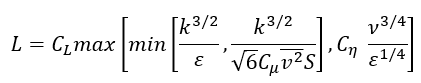
湍流时间和长度尺度由标准的 k-ɛ 方程确定:
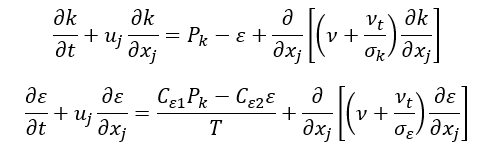
应变率大小定义为:
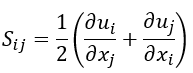
湍动能的产生定义为:
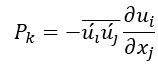
用 y 表示与墙体垂直的坐标,在无滑移边界上,
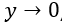
,得出的结果是
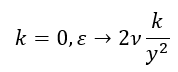
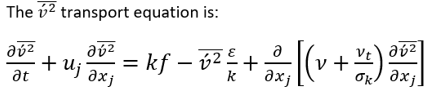
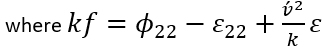
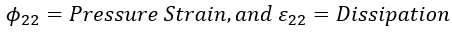
上述方程突出了湍流能量如何从流向分量中重新分配,通过函数 f 的椭圆松弛方程捕获非局部效应。这种方法可确保精确、真实地描述流体中的空间相互作用,为复杂的湍流动力学提供了更深入的见解。
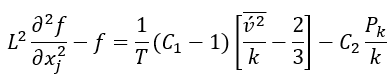
壁面附近的压力-应变
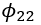
和耗散项
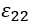
的渐近行为可描述为:
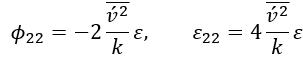
由此得出原始
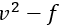
模型中
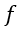
的边界条件为:
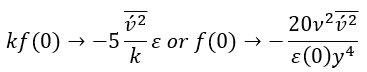
原始模型的系数如下:
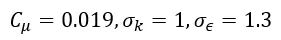
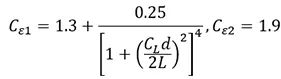
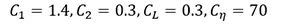
其中 d 是到壁面的距离。
椭圆松弛方法:湍流中的代码友好创新(Lien 和 Durban,1996;Lien 等,1998)。
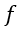
的边界条件包含了一个
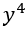
项的四次方,而
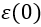
出现在分母上。这在层流和过渡区带来了一个挑战,
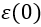
在此处的定义是不适定的,会引起数值振荡。当采用分离数值过程时,这些振荡变得更为明显,因为它能防止
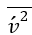
和
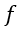
在壁面附近的隐式耦合。这启发人们重新表述了
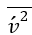
输运方程中的项:
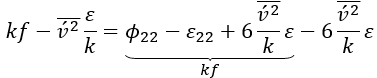
这里重新定义了
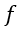
,带来椭圆松弛方程的修改,进而更好地捕捉流体动力学。
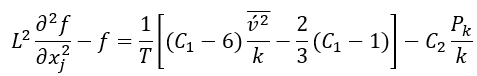
壁面的
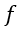
边界条件导致
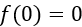
,这大大提高了数值稳定性。
注意,这些修改保留了与原始模型相同的渐近近壁行为
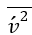
:
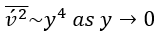
随着
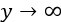
,由椭圆松弛引起的运动阻塞效应消失。
得出的代码友好型模型的常量表示为: