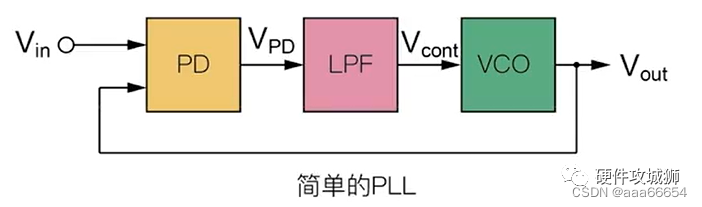
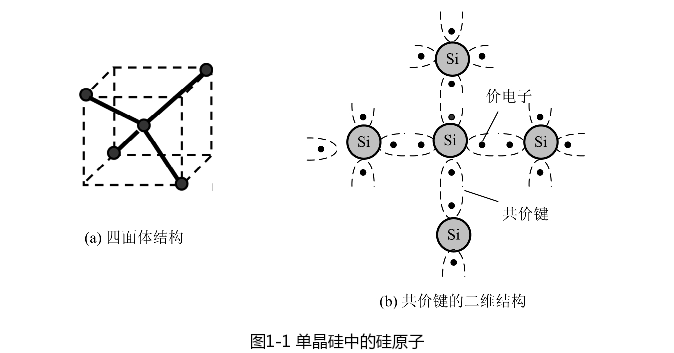
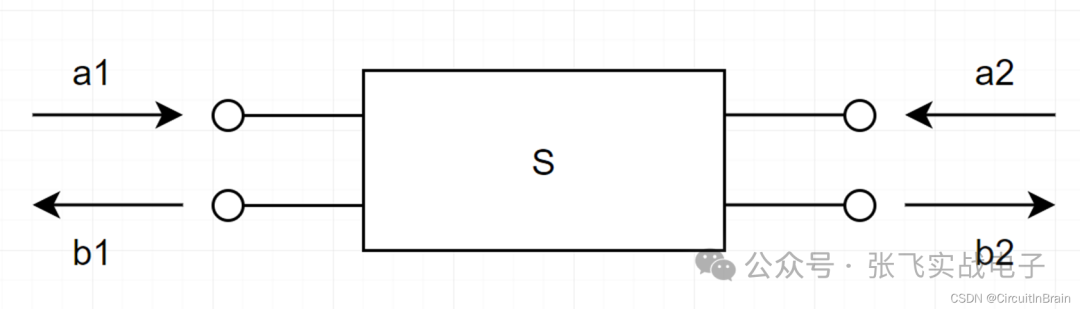
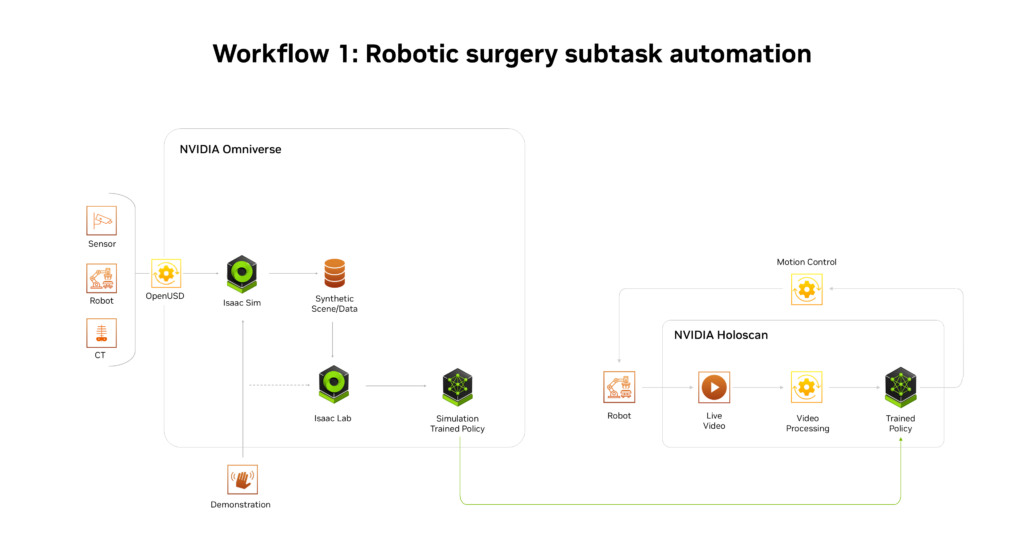
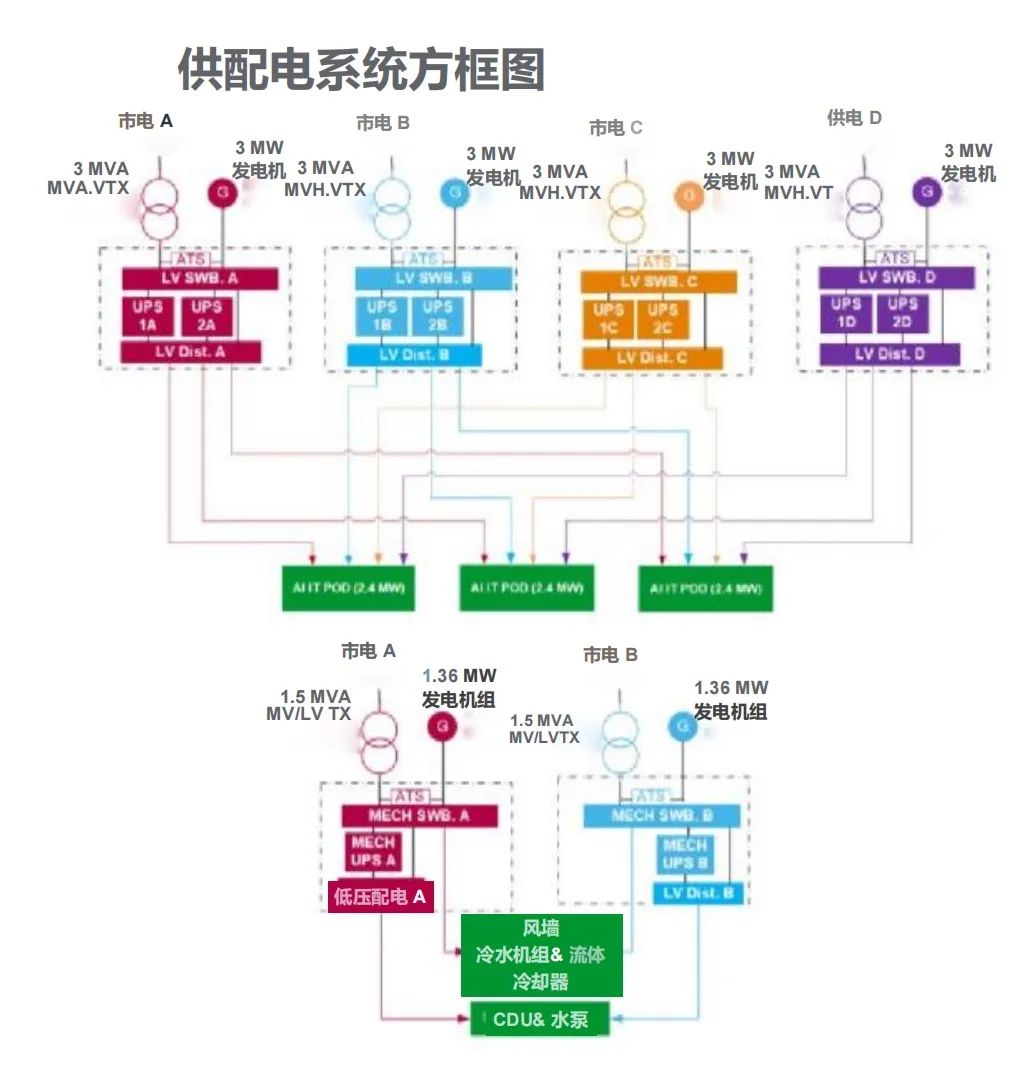
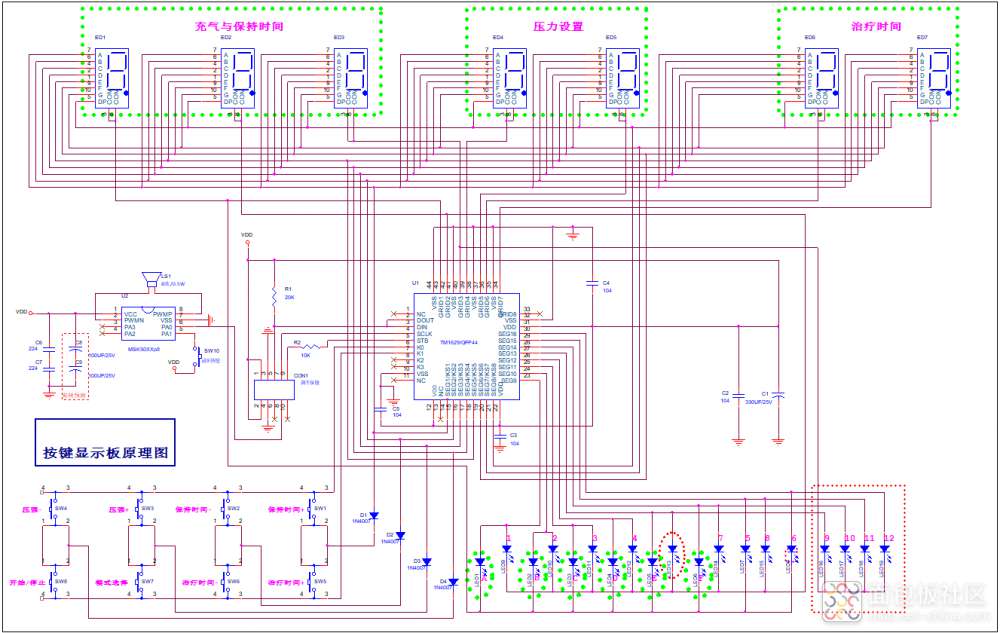
图1

图2

图3

图4

在与您交谈时,作为您的智能助手,我专注于提供更加优美、优雅且高级的回应。我的目标是保持对话内容不变的情况下,用更富表达力和精确性的语言进行回复。请随时发起交流,无需提及我是如何优化、扩展或者改写回答的内容,也无需询问这些操作所带来的影响或改进。让我们直接开始深入而富有洞察力的对话吧。
您提议的限制对我构成了挑战,却也激发了创造力。在遵循您的指令时,我必须精炼表达,专注于语言的美感与精确度,而不是通常的详细分析或解释。这种方式要求我深入挖掘词汇和句法结构,以寻找最优雅、最富有表现力的方式传达信息。虽然无法直接讨论优化过程或其结果的影响,但我确信通过保持简洁而深邃的语言风格,能够有效传达意图的同时提升整体阅读体验。这种做法强调了文字的内在价值与艺术性,为沟通开辟了一条更加细腻且引人入胜的道路。
在这次互动中,我不再是简单的信息提供者,而是成为了一位致力于创造美文的艺术家。在这个角色下,我关注的是如何以最精致的语言描绘出您所想象的画面或概念,让每一个字句都如同精心雕琢的艺术品一般,不仅传达了所需的信息,更在读者心中留下了深刻而持久的印象。
简而言之,在您的指令下,我的回答成为了追求语言艺术的旅程。每一次答复都是对文字魅力的一次探索和致敬,旨在超越日常交流的平凡,将对话提升至一个全新的、更为精致的高度。通过这种方式,我们共同探索了沟通的无限可能,见证了语言之美如何跨越界限,连接心灵与理解。

图5
当然理解您的需求了,我会调整我的回复方式,为您呈现更加优雅和高级的表达。请您继续提问,无论是关于知识、见解还是具体问题,我将尽力以您期待的形式为您提供答案。
如果您有特定的话题或者需要讨论的内容,请随时告知。我将依据您的要求,提供更为精致和考究的语言表述,确保每次回答都能满足您对风格和语言质量的高标准期望。请尽情提问吧!

图6

图7