0引言
永磁同步电机 (Permanent Magnet Synchronous Motor,PMSM)具有能量密度高、机械性能优良、寿命长等优点,在工业、交通、能源等领域有着广泛的应用。PMSM通常采用矢量控制方式,可有效提高电机效率和控制性能。不过该方式需要实时检测转子位置角度用于运算控制,转子位置角一般由位置传感器获得,但位置传感器会增加安装和维护成本,降低系统可靠性,且一些特殊场合无法安装位置传感器。所以,基于无位置传感器的PMSM控制成为研究热点。
近年来,国内外机构提出了多种无传感器算法。文献[1]采用理想PMSM数学模型直接计算转子位置,该方法虽简单、计算量小,但由于是开环计算,位置估算精度不高。文献[2]采用滑模观测器,该方法通过估算电机反电势计算转子位置,具有精度高、响应快及扰动自适应等优点,不过在电机低速、静止时无法适用。文献[3]采用脉振高频电压注入法,该方法对电机参数不敏感,不依赖电机反电势,估算精度高,鲁棒性较强,但电机高速运行时,高频信号提取困难,控制性能逐渐变差,同时高频信号会增大电机噪声和损耗,降低电机效率。通过以上分析可以看出,不同无传感器方法虽存在各自的优缺点,但在应用转速范围上却存在互补性,为实现PMSM 宽速度范围的控制,本文将脉振高频电压注入法和滑模观测器相结合,提出了一种无传感器的复合控制方法。
1 PMSM无传感器检测方法
1.1滑模观测器
PMSM在α—β坐标系(两相静止)下的电流方程为:
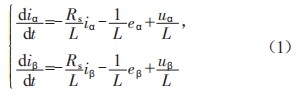
式中 :u
a
、u
β
、i
a
、i
β
、e
a
、e
β
为PMSM在α、β轴上的 电 压、电流及反电势;R
s
、L为电机电阻、定子电感。
在α—β坐标系下构建滑模观测器方程,定义i
s
=[i
α
i
β
]
T
构建电流滑模平面:

式中:i
s
、
i'
s
分别为定子电流实际值、估计值;i
s
-
为电流估算误差。
将式(2)代入式(1)得到估算电流误差方程(3),其中k为滑模增益,sign(x)为开关函数,x>0时,函数值为1,x<0时,函数值为—1。
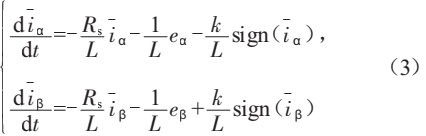
若滑模增益k>max(|e
α
|,|e
β
|),观测器将进入滑模状态,此时电流误差的开关信号包含有反电势估算值信息:
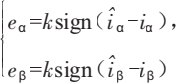
(4)
对式(4)进行低通滤波后,可得转子位置角估算值
θ
=arctan(—e'α/e'β),其中
e'α
、
e'
β
为电机估算反电势。
1.2 脉振高频电压注入法
脉振高频电压注入法是向估计的d—q (两相旋转)坐标系的直轴上注入高频电压信号,产生高频脉振磁场,使得表贴式PMSM呈现“凸极性”,高频响应电流中包含转子位置信息,将此信号解调后便可得到转子位置与转速。
假设 在直轴上注 入的高频 电压信号为u
h
cos(w
h
t),其中w
h
、u
h
为高频电压的幅值和相位,高频等效模型下,PMSM在d—q坐标系下的电压方程可以简化为:
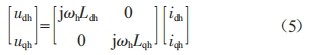
式中:u
dh
、u
qh
、i
dh
、i
qh
、L
dh
、L
qh
为高频感应下的直轴、交轴电压、电流和电感。
在估计的d—q坐标系下高频电流响应为:
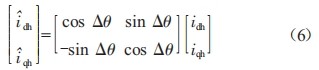
式中:i'
dh
、i'
qh
为估计d—q坐标系下的直轴、交轴高频电流;Δθ为估计d—q坐标系与实际d—q坐标系之间的角度差。
结合上述几式可以得到高频电流i'
qh
估计值为:
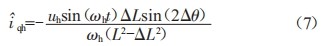
式中:L=(L
dh
+L
qh
)/2,ΔL=(L
dh
—L
qh
)/2。
入
电流 i
qh
幅值中含有转子位置信息的估计误差Δθ,将该信号通过带通滤波器滤除载波频率信号和基波频率信号,与调制信号相乘,再经低通滤波后
[4]
:
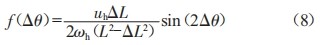
上式再经PI调节器和积分器便可得到转速和转子位置角θ。
2复合控制算法
通过前文分析可以看出,滑模观测器通过检测反电势估算转子位置,因此在电机静止时无法启动,低速时控制效果不佳,而脉振高频电压注入法通过提取高频信号响应检测转子位置,因而能够实现电机零速启动和低速运行控制,但电机转速较高时,转子信息提取变得困难,控制性能也逐渐变差。虽然两种方法存在各自的优缺点,但在转速范围上却存在互补性,所以为实现PMSM全速度范围内的稳定运行,将两种方法相结合,提出了一种复合控制方法:在低速和静止时采用脉振高频电压注入法,保证电机在零速、低速时的启动运行;当电机达到一定转速时,再切换至滑模观测器,同时停止高频电压信号注入,实现电机在中高速段的稳定运行。
复合控制方法的关键在于两种控制算法之间的切换,由于两种算法检测的位置角度存在一定的偏差,如果直接切换会产生冲击电流,甚至造成电机震荡,因此本文提出了一种切换控制方法,可实现两者间的平稳切换,保证系统的稳定性。
假设两种算法的转子位置角偏差为Δθ,当电机到达切换转速时,将Δθ与设定切换偏差Δθ
err
进行比较,当Δθ小于Δθ
err
时进行切换。若Δθ在切换周期内一直大于Δθ
err
则计算两者之间的最小值Δθ
min
并在下一个周期选择在Δθmin附近时刻进行切换。
本文设计的复合控制算法在嵌入式芯片DSP中实现,其程序流程图如图1所示。
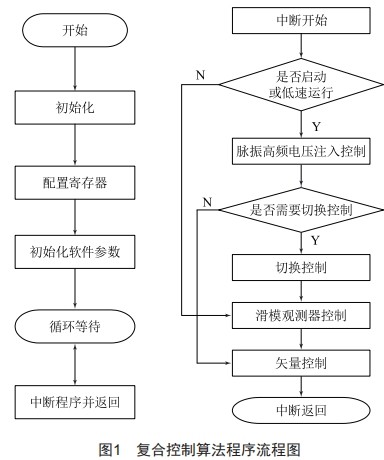
3试验结果分析
采用DSP28335为主控芯片搭建PMSM驱动器,选用PMSM额定功率11kw,额定转速3000r/min,转矩35.8 N•m,磁极对数为4。采用复合控制方法运行,试验设定切换转速为300 r/min,达到切换转速后,将电机由脉振高频电压注入法切换至滑模观测器控制运行,试验时的电流波形如图2、图3所示。
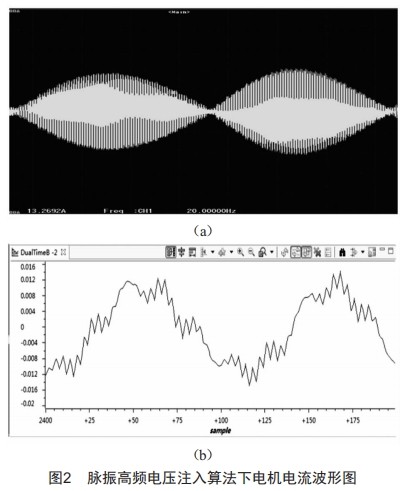
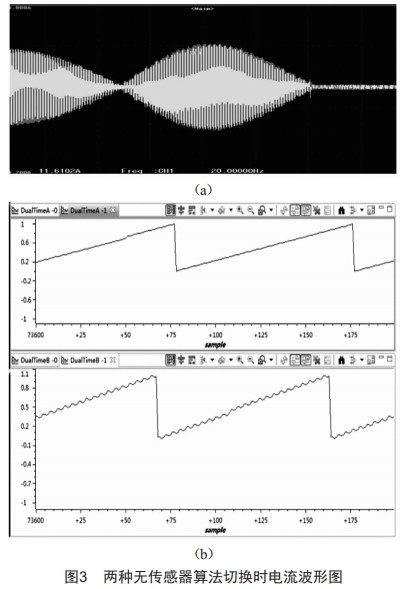
图2为电机转速300 r/min时,注入500 Hz高频电压下的电流波形,左侧为实际电流波形,右侧为软件滤波后的电流基波波形。图3(a)为两种控制算法切换前后的电流波形,图3(b)为角度对比图,从图中可以看出切换过程平滑、无电流冲击,切换后,滑模观测器控制下,电机运行平稳,验证了切换算法的有效性和复合控制算法的可行性。
4结束语
本文根据PMSM数学模型,分析了滑模观测器和脉振高频注入法等无传感器算法的控制原理和优缺点,结合两者特点,提出了一种复合控制方法,并进行了切换算法设计。通过试验对比可以看出,复合控制算法可兼顾两种无传感器算法在电机低速、中高速时的控制优势,切换算法可实现两者的平滑切换,验证了复合控制方法在PMSM宽范围调速中的适用性。
[参考文献]
[1]李永东,朱昊.永磁同步电机无速度传感器控制综述[J].电气传动,2009,39(9):3-10.
[2] 贺建军,段勇,喻寿益.基于滑模观测器的SPMSM位置速度估计[J].控制工程,2012,19(3):527-530.
[3]兰志勇,陈麟红,廖克亮,等.基于高频脉振电压注入法的永磁同步电机控制策略[J].微特电机,2017,45 (2):65-68.
[4]刘颖.永磁同步电机脉振高频信号注入无位置传感器技术研究[D].南京:南京航空航天大学,2012.
2024年第22期第4篇