介绍
这个项目的想法是在我完成数字电子课的一个实验时产生的。目标是创建一个电路,使用开关将4位二进制数作为输入,并将其作为等效的十六进制数输出到七段显示器上。使用Quartus,我们将逻辑门电路编程到FPGA(现场可编程门阵列)上。

为一个看似简单的电路编程,同时了解其设计背后的复杂过程和潜在的二进制运算,这是一件令人着迷的事情。
我决定承担一个更具挑战性的项目,这需要更深入的思考和仔细的计划。有两个想法闪过我的脑海:
•而不是输出只有一个7段显示,使用两个代替
•在设计中限制门的类型为NAND门
为了降低成本,我选择使用物理NAND门集成电路而不是FPGA,后者的成本通常在150美元左右。
我对额外的挑战很满意。因此,我的目标是创建一个电路,接受4位二进制输入,并仅使用NAND门输出等效的十进制数。
Ben Eater关于设计7段解码器的视频是另一个灵感来源。
设计过程
我计划使用的7段显示是一个共同的阳极,这是有效的低。
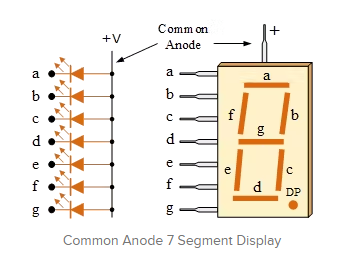
活动低电平意味着逻辑低电平输入激活相应的段。如果我想打开“a”段,则需要将低电压(约0V)应用于“a”引脚。
创建真值表有助于理解哪些输入组合对应于输出。
作为参考,表中的1表示逻辑级别高,0表示逻辑级别低。
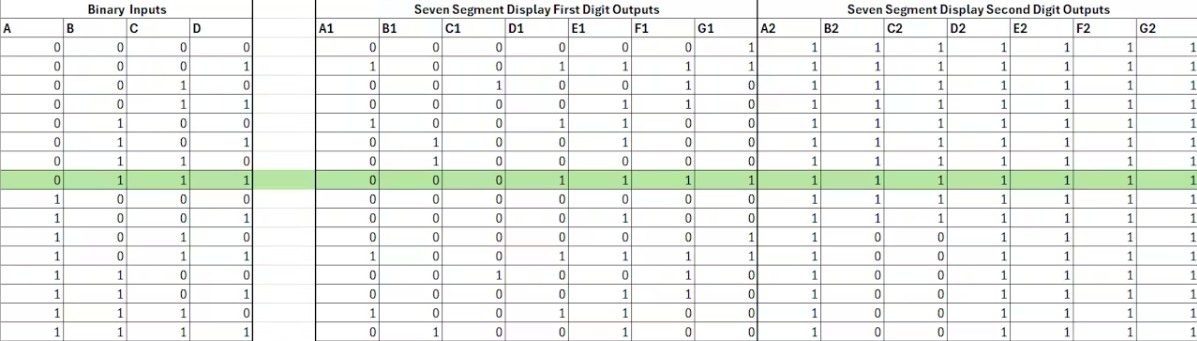
真值表
输出中的前七列表示七段显示中的一位,而后七列对应于十位。
对于输入部分,每行对应一个等效的十进制数。
例如,二进制输入0111转换为十进制数7,如真值表中突出显示的部分所示。所以,七段显示看起来是这样的。

7段显示数字7
对于二进制输入0111,第一个数字需要段a、b和c亮起,因此需要一个低逻辑电平(0)来激活这些段。这可以从真值表中看出。
因此,为了将这些输入和输出组合转换成电路,使用了k映射和布尔方程。
K映射是一种将真值表的输入和输出组合转换为简化形式的布尔方程的方法。
然后,布尔方程可以用不同的逻辑门转换成电路。
例如,让我们关注E1列。
E1的K映射是这样的。
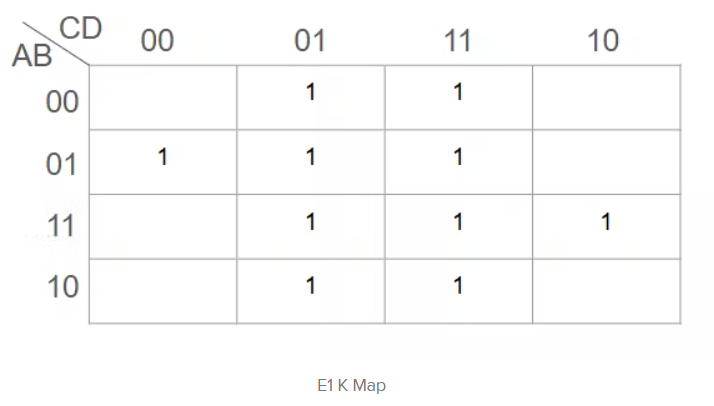
“AB”下最左边的值是输入AB的不同组合。“A”值是第一个数字,而“B”值是第二个数字。同样的事情也发生在“CD”右侧上方的值上。“C”值是第一个数字,“D”值是第二个数字。
使用真值表时,只要E1列中有1,就会在K Map的相应框中填充一个“1”。例如,输入0001,输出是1,其中K映射的第一行和第二列框中有一个1。
下一步是把这些“1”分成2、4或8组。这些基团之间可能有一些重叠,看起来像这样。
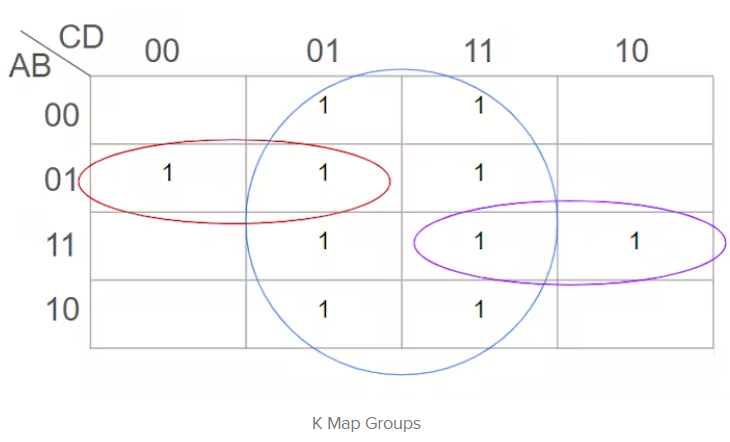
利用这些群,可以形成布尔方程。
从红色组开始,当看AB列时,“1”不移到另一行。这些1留在01行。这意味着A和B保持不变。当查看CD行时,‘1’从‘00’列移动到‘01’列。移动列时唯一改变的是最后一个数字(D)从0变为1。这意味着C保持不变,但D改变了。
A保持0。B保持1。C保持0。
我们可以将变量B保持为布尔形式,因为它的值为1。
但是为了用布尔形式表示变量‘A’,它被表示为‘Ā’以表示它的值为0。对于变量C也是一样。
红色组表示的布尔项是ĀBC。注意,这一项只包括不变的变量。D不是这一项的一部分。
有了最终的布尔方程E1 = ĀBC′s + D + ABC,我们可以进一步简化它,使其更容易转换为NAND门电路。使用双补语和德摩根定理就可以做到这一点。
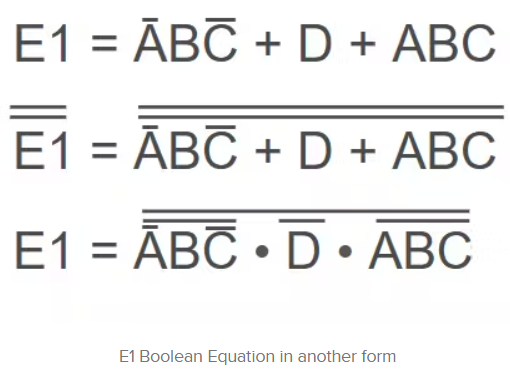
第二个方程显示了一个双补。这个技巧被用来帮助建立第三个方程,它使用了德摩根定理。这个定理改变了乘法的加法,打破了第一个补。
这个方程现在是一个很容易使用NAND门的形式。所以最终的电路看起来是这样的。
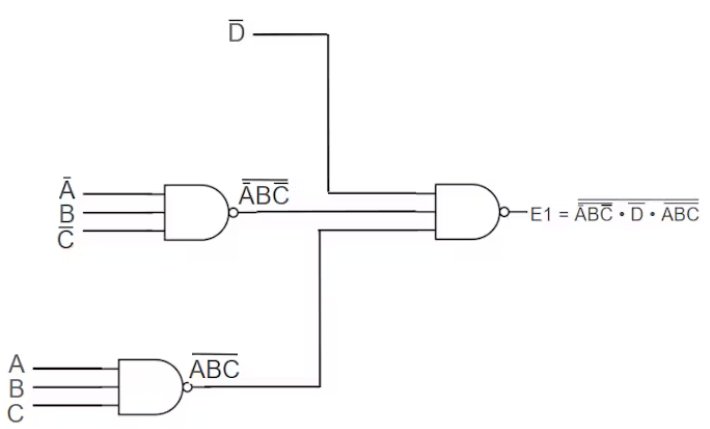
具有3个输入非与门的E1电路
然后,为了将3个输入NAND门变为2个输入NAND门,使用De Morgan定理将3项变量分解为2项或更少的组。我已经分配了单独的变量(F, G和H),以便更容易理解。
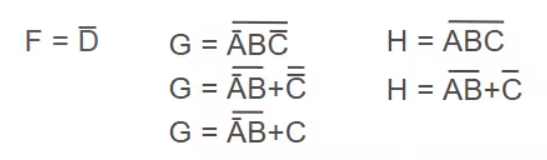
简化布尔项
然后将E1处的最后3个输入NAND门分解,将方程变换为:
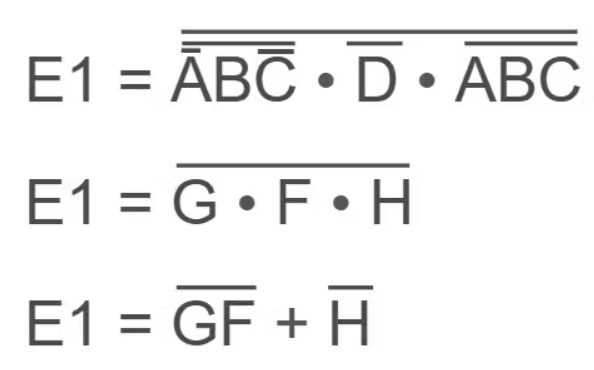
E1的最终布尔方程
然后使用这些NAND等效的OR门和NOT门:
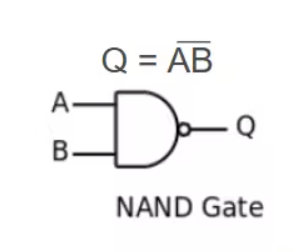
与非门
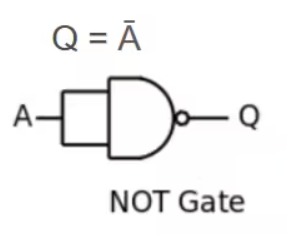
非门等效
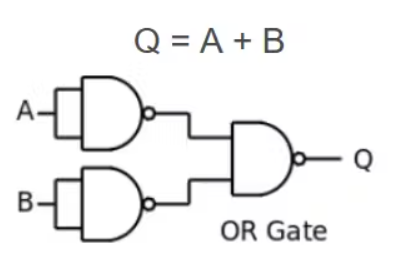
或门等效
从真值表到电路的过程在7段显示器的每个引脚上重复。下面是在Quartus上为每个引脚设计的其他最终电路。
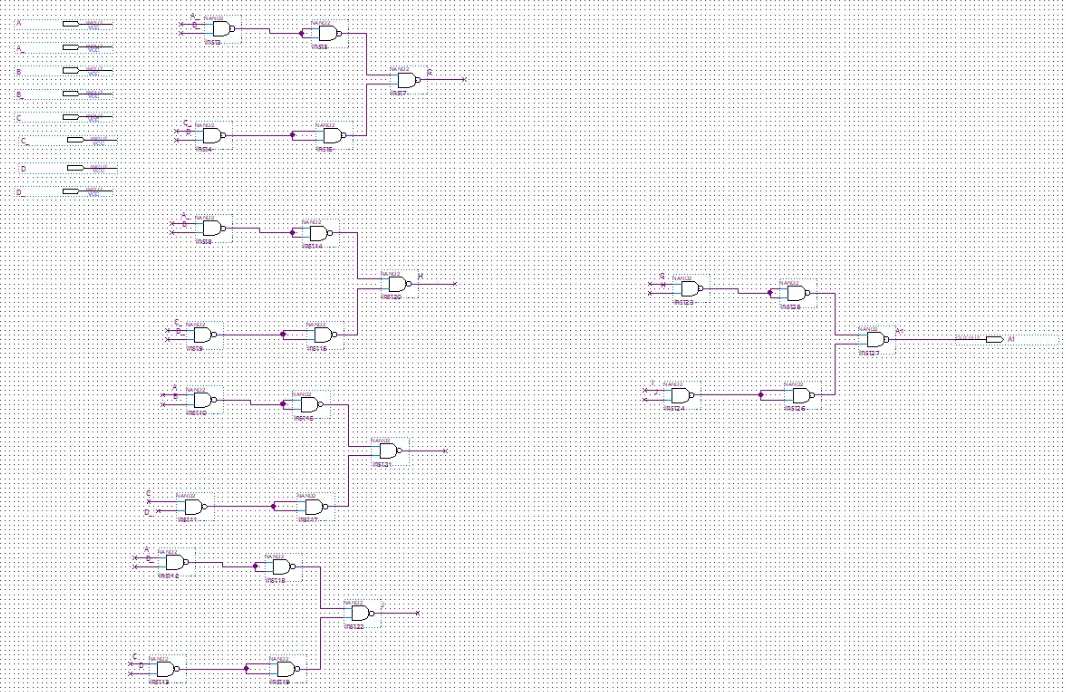
A1引脚电路
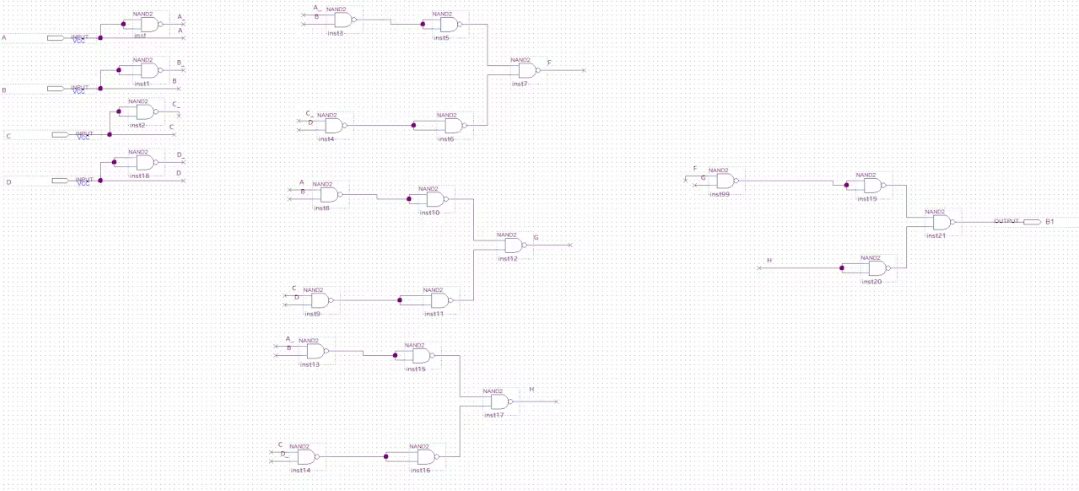
B1引脚电路
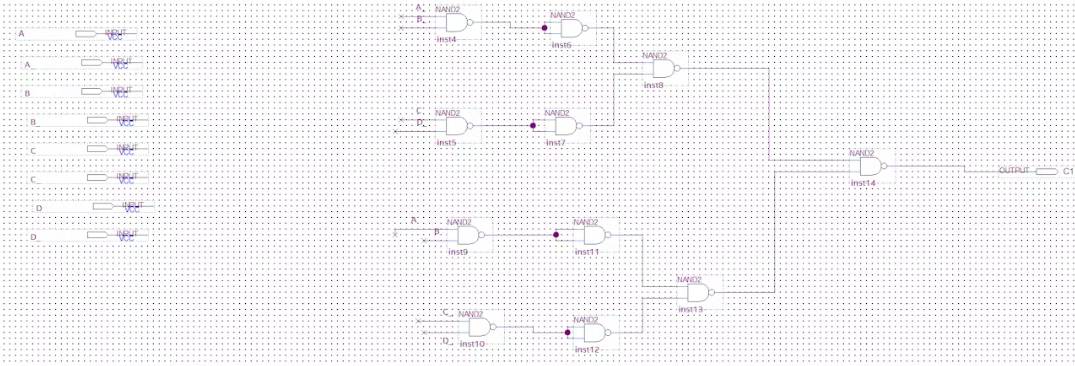
C1引脚电路
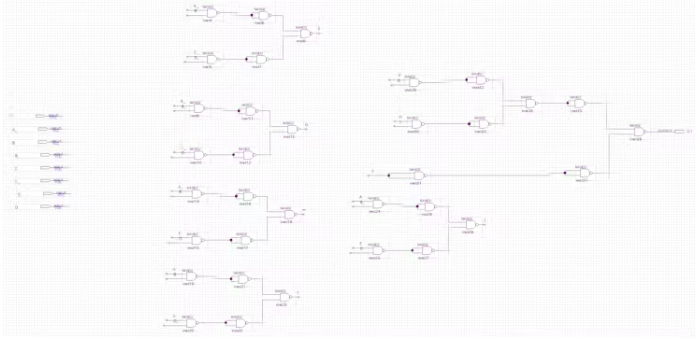
引脚D1电路
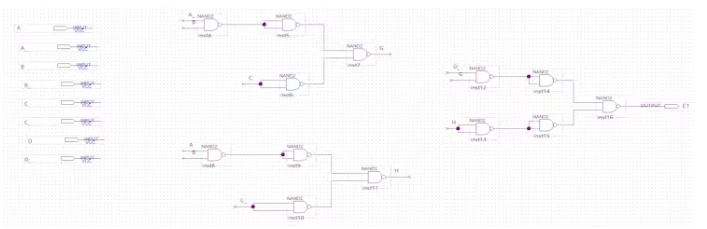
E1引脚电路
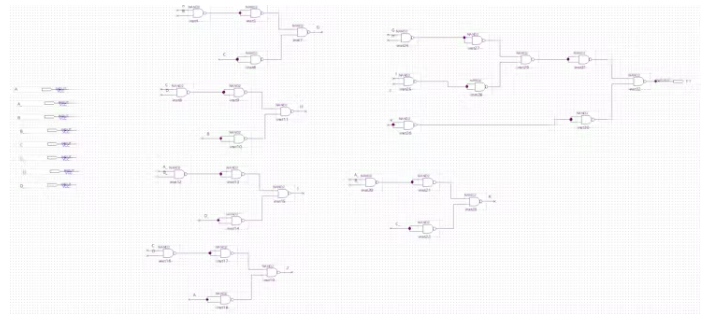
F1引脚电路
G1引脚电路
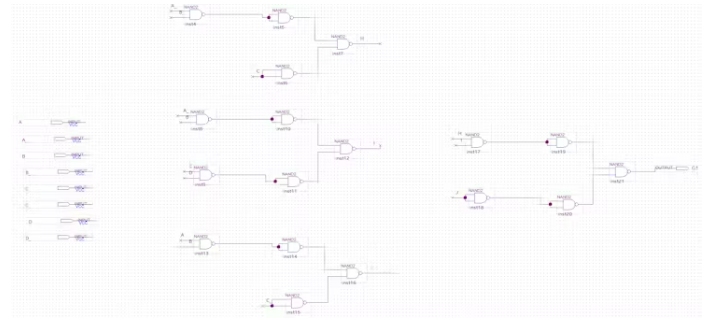
引脚B2和C2的电路
所有其他引脚(A2, D2, E2等)都连接到高逻辑电平输出,因为这些引脚保持关闭状态。它们不需要任何带NAND门的电路。
使用这些电路,总共需要157个NAND门。
TinkerCAD电路也用于在面包板上构建电路,因此我可以在稍后的构建过程中轻松地复制它们。该软件没有单独的NAND门组件,但它有这些称为ic(集成电路)的黑色块,这些特定的ic有4个带有这些引脚的NAND门,如下所示。
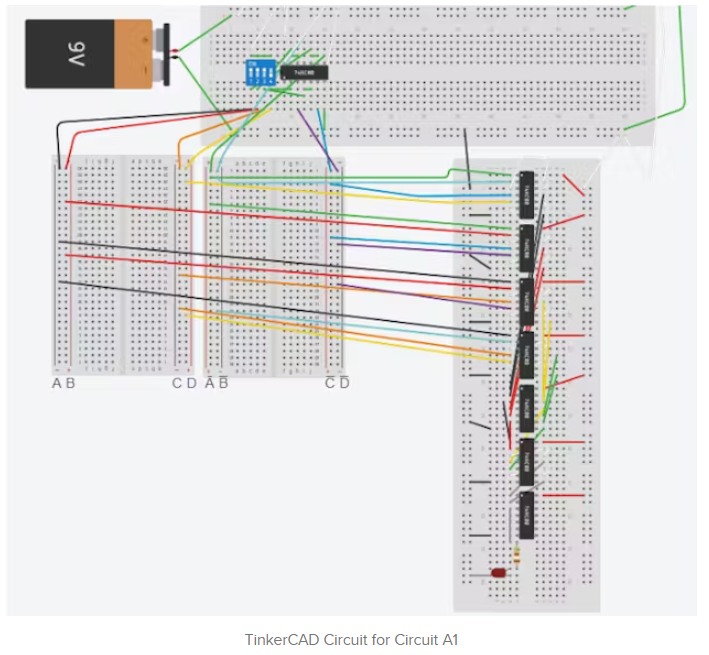
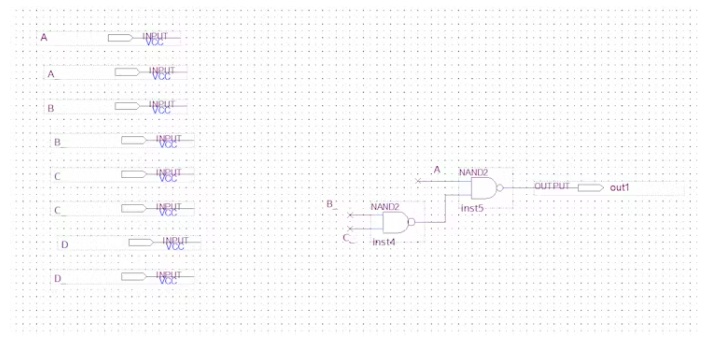
这是我在TinkerCAD中为A1电路构建的电路。四个开关对应四个位(ABCD),并连接到其右侧的NAND门。NAND门作为四个非门产生相反的输出(它是产生Ā B′C′和D′的那些)
左边的两个面包板是输出和对应输出的轨道。然后连接到右边的非与门,但是它显示在引脚A1的电路的前面的图中。这条轨道也将被所有其他电路使用。
为了验证设置,将LED连接到输出端。对输入组合(ABCD)进行测试,并将结果与A1列的真值表进行比较。如果所有的组合都符合LED打开和关闭的时间,则设置良好。
在所有其他电路中重复了这一模拟。
在模拟并确认每个电路产生正确的输出后,我开始构建过程。
构建过程
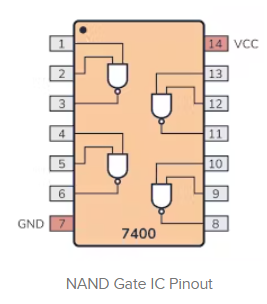
我使用的NAND门IC是TI SN74HC00N。它是一个具有4个NAND门的IC,与模拟中的引脚相同。
每个IC包含4个NAND门,该项目需要40个IC,成本约为25美元。
该项目需要多个面包板和大量的电线。为了降低成本,我重新利用了我爸爸到处放着的5类电缆,剪断并解开电线,这被证明是一项耗时的任务。

每个电路都是根据TinkderCad电路模拟构建的,并且在末端附加了一个LED,以确保产生正确的输出,并与真值表进行检查。
在每一个电路确认工作后,我把它安全地放在一边,开始另一个电路的工作。在每个电路建成后,所有电路都连接在一起,并连接到适当的引脚上,以连接七段显示器。
在这个项目结束时,这是最终的结果:

最终的想法
最难完成的任务之一是调试LED输出与真值表不匹配的情况。一开始很令人沮丧,但慢慢地,我花时间仔细检查每根电线和每个引脚,确保每个电路都成功。
这个项目的另一个困难部分是在建造过程中失去动力。我的一部分只是想买电线,这样我就不必花额外的时间切割,解开和剥离第5类电线,但只要一步一步地推进这个过程,就能帮助我到达终点。
但我在这个项目中最大的乐趣肯定是在设计过程中。我喜欢用不同的工具和方法解决一个难题,从a点到b点。这个问题在一天内可以解决的地方不太容易,但在看起来不可能解决的地方也不太难。这是一种合适的难度,足够具有挑战性,它要求我确保一切都是正确的。
最后,我很高兴我完成了这个项目。这个项目让我意识到我们今天使用的技术的复杂性,以及对这些硬件和不断开发和改进这些东西的人的赞赏。
在整个项目中,我在设计、构建和测试阶段学到了很多东西。此外,能够很好地记录它对我来说是一个巨大的学习曲线。我知道在写文件的过程中我可以做很多改进,比如简化一些解释,在构建过程中使用合适的图片,编写吸引人的材料等等。但我希望不断进步,不断学习,保持好奇心。
现在我只需要找个地方放这东西。
本文编译自hackster.io